Tálec si pred odchodom do školy odložil svoj mamutí kel. Keď prišiel zo školy, kel bol fuč. Pri jeho hľadaní vyspovedal aj svojich kamarátov. Vedel, že jeden z nich klame a zvyšní hovoria pravdu. Toto mu povedali:

• Sapi: Tvoj kel má Ens.
• Ens: Neo kel nemá.
• Neo: Ander ti klame.
• Ander: Sapi má tvoj kel.

Ander kreslil na stenu jaskyne trojuholník $ABC$. Stred strany $AC$ označil $E$ a stred strany $BC$ označil $F$. Na priamke $EF$ leží bod $G$ taký, že $|EF| = |FG|$ pričom body $E$ a $G$ sú rôzne. Veľkosť uhla $FEA$ je $108$ stupňov a veľkosť uhla $ABC$ je $36$ stupňov. Aká je veľkosť uhla $BGC$?

Neo a Tálec hrali hru. Najprv Neo napísal čísla $1$ až $6$ do vrcholov pravidelného šesťuholníka. Potom si Tálec vybral vrchol a pričítal k nemu čísla v susedných vrcholoch. Tálec dá Neovi toľko mušlí, aký súčet mu vyšiel, pričom platí, že Tálec vyberá vrchol tak, aby dal Neovi čo najmenej mušlí a Neo píše čísla do vrcholov tak, aby dostal čo najviac mušlí. Koľko mušlí dostal Neo? Dokážte, že viac mušlí nemôže dostať.

Vstup do Anderovej jaskyne má tvar rovnostranného trojuholníka $ABC$ so stranou dlhou $48$ stôp. Na strane $AB$ leží bod $E$ a na strane $BC$ ležia postupne body $D$ a $F$ tak, že obsahy trojuholníkov $AFC$, $AEF$, $EDF$ a $EBD$ sú rovnaké. Vypočítajte v stopách súčet dĺžok úsečiek $|EB| + |DB|$.

Neo a Ander si myslia dve rôzne kladné celé čísla. Súčet ich najväčšieho spoločného deliteľa a najmenšieho spoločného násobku je rovný $323$. Aké dvojice čísel si Neo a Ander mohli myslieť? Nájdite všetky možnosti a dokážte, že iné neexistujú.

Ander a Tálec písali do piesku čísla nasledovným spôsobom: Začali dvomi ľubovoľnými číslami a každý ďalší člen vznikol ako súčet cifier predchádzajúcich dvoch členov. Napríklad, ak začneme s číslami 5 a 8, tak začiatok postupnosti vyzerá takto: $5, 8, 13, 12, 7, 10, ...$

• Dokážte, že ak prvé dva členy postupnosti sú ľubovoľné čísla menšie ako milión, tak potom štvrtý aj piaty člen je menší ako 100.
• Dokážte, že ak prvé dva členy postupnosti sú ľubovoľné čísla menšie ako 100, tak v postupnosti existuje člen taký, že všetky za ním nasledujúce čísla sú menšie ako 21.
• Dokážte, že ak prvé dva členy postupnosti sú ľubovoľné čísla menšie ako 100, tak v postupnosti existuje aj člen taký, že všetky za ním nasledujúce čísla sú menšie ako 19.

Ohnisko tvaru obdĺžnika $ABCD$ má stranu $AB$ dlhú $3$ stopy a stranu $BC$ dlhú $1$ stopu. Bod $E$ je vzdialený pol stopy od úsečky $CD$, leží mimo obdĺžnika $ABCD$ a $|CE|=|DE|$. Aká je veľkosť uhla $AEB$?

U Nea na narodeninovej oslave sú chlapci a dievčatá a každý s každým sa buď pozná, alebo nepozná (je to vzájomné). Vieme, že na oslave je $12$ chlapcov a každý z nich pozná práve $6$ dievčat. Tiež vieme, že každé dievča pozná rovnaký počet chlapcov ako ostatné dievčatá. Koľko je na oslave dievčat? Nájdite všetky možnosti a dokážte, že iné nie sú.

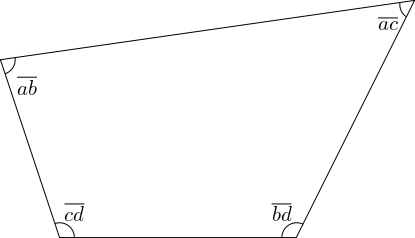
Kožušina z mamuta má tvar štvoruholníka. Veľkosti uhlov štvoruholníka sú čísla zložené z cifier $a,b,c,d$ ako na obrázku. Nájdite všetky možné veľkosti uhlov a vysvetlite, prečo iné veľkosti uhlov nevyhovujú. Obrázok je iba ilustračný.

Tálec s Anderom sa zamýšľali nad domácou úlohou z matematiky. Hľadali všetky prvočísla, ktoré sa nedali zapísať ako súčet dvoch zložených čísel. Pomôžte im ich nájsť a dokážte, že žiadne ďalšie neexistujú.

Neo si zvolil nejaké číslo $k$. Následne k jaskynnej stene prišiel Tálec a napísal nejakých $k+2$ rôznych kladných celých čísel. Dokážte, že medzi číslami na stene sa určite nachádza buď dvojica čísel s rozdielom deliteľným $2k$, alebo dvojica čísel so súčtom deliteľným $2k$.

Hrot Anderovho oštepa je tvaru trojuholníka $ABC$, kde dĺžka úsečky $AC$ je $12$ palcov a veľkosť uhla $ACB$ je $120$ stupňov. Os tohto uhla pretína stranu $AB$ v bode $D$. Taktiež vieme, že $|AE|=|EC|=|CB|$, kde $E$ je stred strany $AC$. Koľko palcov má úsečka $CD$? Dĺžku je potrebné vyjadriť presne, a teda bez pomoci rysovania.