Chulio a Vincenzo sú známi svojou záletnou povahou. Aby sa ich ženy o ničom od nikoho nedozvedeli, v niektoré dni každému klamú, zatiaľ čo zvyšné dni vravia pravdu. Chulio klame vždy len v stredu, sobotu a nedeľu a Vincenzo hovorí pravdu len v stredu, štvrtok a sobotu. Keď sa stretli v predsieni Palazzo di Arcobaleno, prebehol tento rozhovor:

• Chulio: Buongiorno! Včera som klamal!
• Vincenzo: Ciao! Aj ja!

Francesca dostala od Vincenza na výročie amulet s tromi tajnými prepážkami. Amulet má tvar trojuholníka $ABC$. Označme stredy strán $CB$ a $CA$ písmenami $K$ a $L$. Prepážka s jedom pripraveným pre Biancu tvaru štvoruholníka $ABKL$ má obvod $10cm$ a prepážka s fotkou Chulia tvaru trojuholníka $KLC$ má obvod $6cm$. Aká je dĺžka tretej tajnej prepážky tvaru úsečky $KL$?

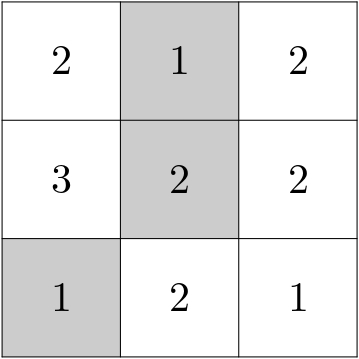
Záhrada Palazzo di Arcobaleno je rozdelená na deväť záhonov oddelených chodníčkami a usporiadaných do štvorca $3\times3$. Niektoré záhony sú uzavreté pre verejnosť (zaznačené na plániku sivou farbou). Do každého záhonu v plániku sme vpísali číslo označujúce počet uzavretých záhonov (sivých políčok), s ktorými daný záhon susedí, či už chodníčkom alebo rohom. Na obrázku vidíte príklad, ako môže vyzerať plánik, v ktorom je súčet čísel v záhonoch $16$. Zistite, koľko existuje rôznych možností, ako uzavrieť záhony, aby sme na plániku mali súčet čísel $17$ (pričom uzavretia záhonov, ktoré vznikli otočením jedného uzavretia, rátame za tie isté).

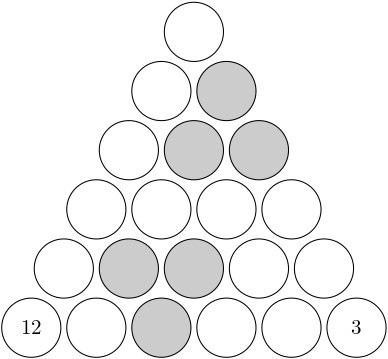
Obrus, do ktorého Francesca vyšíva, má tvar trojuholníka zloženého z kruhov ako na obrázku. Francesca chce vyšiť do každého kruhu toľko kvietkov, aby bol počet kvietkov v každej trojici kruhov, ktoré tvoria malý trojuholník (na obrázku vidíte vyfarbené príklady dvoch takých trojuholníkov) deliteľný piatimi. Do kruhov v dolných rohoch jej však ráno od zlosti Bianca vyšila $12$ kvietkov a $3$ kvietky. Aké rôzne počty kvietkov môže Francesca vyšiť do najvrchnejšieho kruhu? Nájdite všetky možnosti.

Biancina mama Zita je už stará a potrebuje sa každé ráno prejsť do Parco Innamorato. Jej bežná trasa má tvar trojuholníka $ABC$, v ktorom uhol $CAB$ je dvakrát väčší ako uhol $ABC$ a zároveň uhol $ABC$ je menší ako $45$ stupňov. Os uhla $CAB$ pretína stranu $BC$ v bode $D$. Bod $E$ leží na priamke $AD$, ale mimo trojuholníka $ABC$ tak, že veľkosť uhla $BEA$ je 90 stupňov. Keď predĺžime úsečky $AC$ a $BE$ na~priamky, tak sa pretnú v bode $P$. Koľkokrát väčší je uhol $BDP$ ako uhol $ABC$?

Chulio a Vincenzo sa pohádali a rozhodli sa svoj spor vyriešiť súbojom myslí. Hrajú teda hru, kde od mamy Zity dostanú obrázok s $n \geq 3$ bodmi a $k$ úsečkami s koncovými bodmi v týchto bodoch. Najprv Chulio vyberie dva z týchto bodov a označí ich $A$ a $B$ a položí kamienok na bod $A$. Potom hru začína ťahom Vincenzo -- jeho ťah vyzerá tak, že posunie kameň po nejakej úsečke do jej druhého koncového bodu. Nasleduje Chuliov ťah -- zmaže jednu z úsečiek z obrázka. V týchto ťahoch sa postupne striedajú. Ak sa kamienok po nejakom počte ťahov presunie do bodu $B$, tak vyhrá Vincenzo a naopak vyhrá Chulio. Pri zadanej hodnote $n$, aké je najväčšie možné $k$ také, že Chulio vie vždy vyhrať?

Prednedávnom si ešte traja bratia Chulio, Vincenzo a Giovanni Tortelliniovci rozdeľovali rodinné peniaze v pomere $4 : 5 : 6$, najmenej dostával mladý Chulio a najviac najstarší Giovanni. Po tom, ako Giovanniho našli mŕtveho vo vlastnej komnate, Chulio navrhol, že si Giovanniho časť rozdelia s Vincenzom na polovice. Vincenzo však trval na tom, aby si aj túto časť rozdelili nerovnomerne ako zvyčajne, teda v pomere $4 : 5$. Vincenzo by totiž podľa Chuliovho návrhu dostal o $4000$ lýr menej ako podľa svojho. Koľko peňazí má dokopy rodina Tortelliniovcov?

Na maškarné bály v Palazzo di Arcobaleno je každý rok pozvaných $21$ hostí. Na posledných dvoch báloch sa zakaždým rozdelili do troch sál po sedem hostí. Ukážte, že niektorí traja hostia boli na oboch báloch spolu v jednej sále.

Bianca prišla na to, že ju Vincenzo podvádza a tak sa s ním pohádala, že lietali taniere. Konkrétne lietal jeden tanier tvaru konvexného $101$-uholníka. Najprv hodila tanier o zem Bianca a tým ho rozdelila pozdĺž ľubovoľnej uhlopriečky (Bianca aj Vincenzo vedia vždy hodiť tanier tak, aby sa rozdelil pozdĺž nimi zvolenej uhlopriečky) na dva mnohouholníky. Následne Vincenzo zobral zo zeme jeden z črepov tvaru mnohouholníka a znova ho hodom o zem roztrieštil na dva mnohouholníkové črepy pozdĺž ním zvolenej uhlopriečky. Takto striedavo hádžu črepy o zem, pričom hádku prehrá ten, kto už nemôže rozbiť žiaden črep. Kto z nich má vyhrávajúcu stratégiu a akú? Svoju odpoveď zdôvodnite.

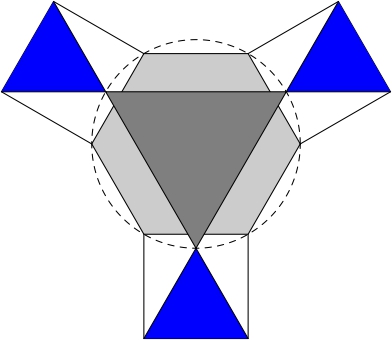
Na obrázku vidíte plán Palazzo di Arcobaleno zložený z pravidelných mnohouholníkov. Sála na prízemí tvaru šesťuholníka a jedáleň na prvom poschodí tvaru tmavosivého trojuholníka sú vpísané do tej istej kružnice. Každá z troch rovnakých komnát tvaru modrého trojuholníka má obsah $17$. Určte obsah jedálne.

Pali si do zošita na nočnom stolíku po každej epizóde zapisuje, koľkokrát už Francesca podviedla Chulia. Prvé dve čísla, ktoré napísal sú $1$ a $1$. Každé nasledujúce číslo, ktoré si zapísal, bolo súčinom predchádzajúcich dvoch zvýšeným o $1$. To znamená, že číslo, čo si napísal po tretej epizóde je $1\cdot1 + 1 = 2$. Ukážte, že číslo, čo si napísal po $2020$-tej epizóde, nie je deliteľné číslom 4.

Vo finále 23tej série sa Vincenzo dozvedá, že Bianca ho podviedla a rozhodol sa zavraždiť ju, rovnako ako posla tejto správy -- Chulia. Naháňajú sa teda po obvode kruhovej sály, pričom Vincenzo obehne celú sálu za $360$ sekúnd. Bianca beží dvakrát rýchlejšie ako Vincenzo a Chulio beží trikrát rýchlejšie ako Vincenzo. Začínajú z rovnakého miesta a behajú, pokým sa znovu všetci traja nestretnú na tom istom mieste. Akú dlhú dobu dokopy za tento čas bol trojuholník Vincenzo-Bianca-Chulio ostrouhlý?