Peťo pracuje v stavebninách a zvolal na pondelok pracovnú poradu. Prišlo na ňu desať jeho podriadených. Všetci z nich majú práve jeden obľúbený druh náradia, a to kladivo, vŕtačku alebo skrutkovač. Keď sa ich Peťo opýtal, kto má rád kladivá, zdvihli ruky všetci desiati. Za skrutkovače zdvihla ruku len polovica z nich, no a napokon za vŕtačku hlasoval len jeden. Peťo si nespomenul, že je pondelok a tak zabudol, že niektorí jeho podriadení celý deň klamú (ostatní hovoria pravdu). Zistite, koľko ľudí obľubuje ktoré náradie.

Pozor! Do znenia úlohy sme doplnili vyznačenú časť, aby bolo zadanie jednoznačné.

Peťo mal vo svojej kancelárii plán novej súčiastky v tvare šesťuholníka. Na pláne bolo na každej hrane vyznačené číslo. Peťo do každého z vrcholov súčiastky vpísal súčet čísel na hranách, ktoré do daného vrcholu vchádzajú. Danovi prezradil, že do vrcholov zaradom napísal čísla: $65$, $139$, $94$, $80$, $139$. Na šiestu hodnotu si však nevedel spomenúť. Aká bola hodnota v šiestom vrchole?

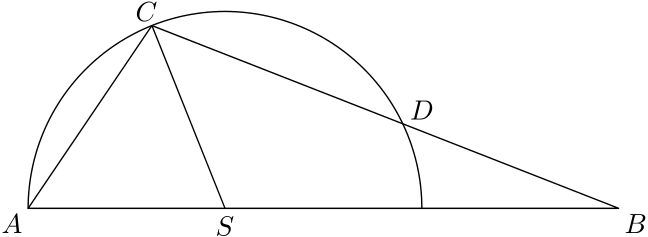
Peťo sa dostal k návrhu novej predajne. Jej pôdorys má tvar kružnice so stredom $S$ a bodmi $A$, $B$, $C$ a $D$ ako na obrázku. Peťovi šéf povedal, že úsečky $SC$ a $BD$ sú rovnako dlhé. V akom pomere sú veľkosti uhlov $ASC$ a $SCD$?

Peťo má francúzske kľúče očíslované číslami od $1$ do $81$. Chce si ich všetky uložiť do priehradiek na pracovnom stole. Priehradky sú usporiadané v mriežke $9\times 9$ a do každej z nich sa vojde práve jeden kľúč. Ukážte, že akokoľvek Peťo vloží kľúče do priehradiek, vieme nájsť číslo $k$ také, že súčin čísel kľúčov v $k$-tom riadku a v $k$-tom stĺpci je rôzny.

Peťo sa chce stretnúť s kolegom Danom na poschodí s kanceláriami. Kancelárie sú usporiadané v mriežke s rozmermi $m\times n$. Dano sa nachádza v opačnom rohu poschodia ako Peťo. Každú minútu sa Peťo a Dano presunú do miestnosti, ktorá je diagonálne od kancelárie, v ktorej boli predtým. Pre aké hodnoty $m$ a $n$ sa vedia Peťo a Dano stretnúť v rovnakej miestnosti? Ako to vedia urobiť? Pre ktoré to nie je možné a prečo?

Peťovi a jeho kolegovi Danovi zvýšil nejaký voľný čas počas obednej pauzy. Na papier si napísali čísla od $1$ do $100$. Postupne sa striedajú v ukladaní znamienok $+$, $-$ a $\times$ do medzier medzi číslami. Peťo ide prvý a hrajú dovtedy, kým nie sú všetky medzery vyplnené. Pred každou hrou si vyžrebujú, kto vyhrá, keď je výsledný výraz na tabuli párny. Má niektorý z nich vyhrávajúcu stratégiu? Ak áno, akú? Ak nie, prečo?

Peťo dostal od šéfa úlohu objednať štyri vrtáky. Peťov šéf si však nepamätal všetky detaily, tak Peťovi o ich veľkostiach povedal len toľko:

• „Ich súčet je 40.“
• „Sú medzi nimi práve dve prvočísla.“
• „Najväčšia z veľkostí je druhá mocnina prirodzeného čísla (číslo vynásobené samo so sebou).“
• „Žiadne dve veľkosti nie sú súdeliteľné (nemajú spoločného deliteľa väčšieho ako 1).“

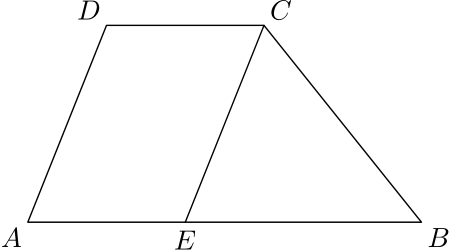
Peťo bol privolaný ako pomocník na stavbu. Stavebný pozemok má tvar lichobežníka $ABCD$, ktorý je rozdelený úsečkou $CE$ na trojuholník a rovnobežník. Bod $F$ je stredom úsečky $CE$. Priamka $DF$ prechádza stredom úsečky $BE$. Obsah trojuholníka $CDE$ je \(\SI{6}{\metre\squared}\). Pomôžte Peťovi určiť obsah pozemku.

Peťo sa s kolegom Danom počas nudných dní hrajú hru. Na začiatku majú dve kôpky, na ktorých je $42$ a $47$ skrutiek. V jednom ťahu musí hráč zobrať jednu kôpku, zahodiť ju, a tú druhú rozdeliť na dve neprázdne kôpky. Ak niekto nevie urobiť žiaden ťah, prehral. Ako prvý je na ťahu Peťo. Kto má víťaznú stratégiu, a aká je?

Na firemnom večierku počítač generoval čísla víťazov tomboly. Postupne generoval rôzne prvočísla, až kým nevygeneroval také, ktoré sa líšilo od nejakého už vygenerovaného o násobok $30$. Koľko najviac čísel mohol vygenerovať?

Stavbári majú v chladničke na začiatku dňa tri typy obedov: sviečková, klobása a rezeň. Vždy, keď robotník otvorí chladničku, vyberie si z nej $2$ obedy rôznych typov a vloží do nej obed tretieho typu. Robotníci chodia do chladničky kým môžu opakovať uvedený postup. Ak na konci dňa zvýši v chladničke iba jeden obed, donesie ho Dano Peťovi. Ukážte, že ak by sa Peťo ráno pozrel do chladničky, vedel by zistiť či mu Dano donesie obed a ak áno, aký typ obeda to bude, bez ohľadu na voľby jednotlivých robotníkov.

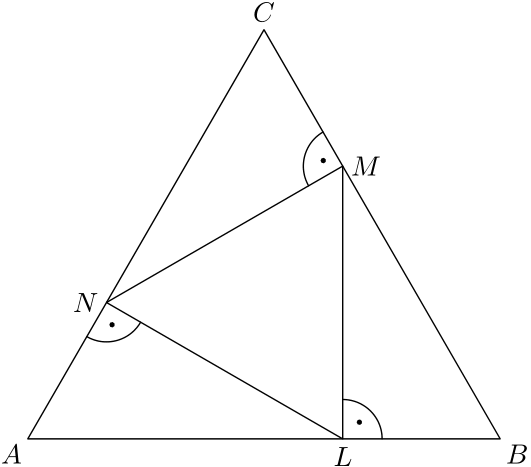
Peťo nebol v poslednej dobe veľmi pracovne vyťažený, preto sa jeho šéf rozhodol dať mu za úlohu navrhnúť nové logo stavebnín. Peťov návrh mal tvar rovnostranného trojuholníka $ABC$ s bodmi $L$, $M$, $N$ ležiacimi postupne na stranách $AB$, $CB$, $CA$, tak, že $ML\perp AB$, $MN\perp CB$ a $LN\perp CA$. Peťo chce, aby bol trojuholník $LMN$ farebný, no nemôže si ale dovoliť minúť priveľa farby. Pomôžte Peťovi zistiť aká časť obsahu loga bude farebná.