Putá sú tvaru rovnoramenného trojuholníka $ABC$. Jeho ramená $AC$ a $BC$ zvierajú uhol veľkosti $36$ stupňov. Os uhla $CAB$ pretína stranu $BC$ v bode $D$. Úsečka $CD$ má dĺžku $8$. Akú dĺžku má strana $AB$?

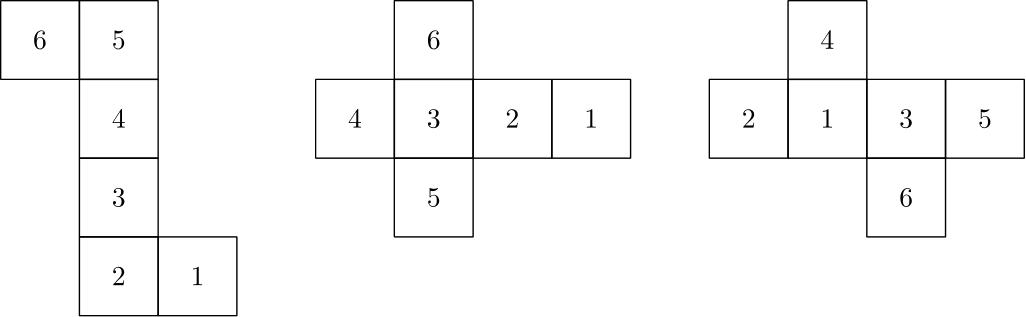
Zo sietí na obrázku možno zostrojiť $3$ kocky. Ak z nich postavíme stĺpček (položíme všetky tri kocky na seba, pričom môžeme kockami ľubovoľne otáčať a meniť ich poradie), na jeho bokoch môžeme (zhora dolu) prečítať štyri trojciferné čísla. Keď tieto štyri čísla sčítame, aký najvačší súčet môžeme dostať? Ako budú tieto kocky vyzerať? Nakreslite ich tak, aby bolo jasné, ktoré strany spolu susedia, a ktoré nie.

Napíšte niekoľko prirodzených čísel do radu tak, že súčet ľubovoľnej $17$-tice susedných čísel bude párny a zároveň ľubovoľnej $18$-tice susedných čísel bude nepárny. Koľko najviac čísel môže byť v rade?

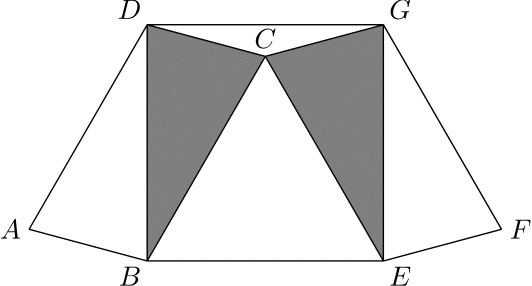
Miestnosť má tvar šesťuholníka $ABEFGD$. Štvoruholníky $ABCD$ a $EFGC$ sú zhodné obdĺžniky a štvoruholník $BEGD$ je tiež obdĺžnik. Určte pomer obsahov bielej a sivej časti šesťuholníka $ABEFGD$, ak trojuholník $BEC$ je rovnostranný.

Heslo je stojedenáste prirodzené číslo $x$, pre ktoré platí, že $32x+18$ a $31x+25$ je deliteľné $11$. Aké je heslo?

"Je $10$ kanálov, ale žiadne dva nie sú prepojené poriadnym tunelom. Vydávam rozkaz, aby sa z každého kanálu prehrabali $4$ poriadne tunely vedúce do iných $4$ kanálov." Bude možné po realizácii tohto plánu prejsť do všetkých kanálov pomocou poriadnych tunelov bez ohľadu na to, ako budú tunely prekopané? Čo ak z každého kanálu pôjde $5$ tunelov?

Jožkovi kamaráti sú zvláštni. Každý z nich buď vždy klame alebo vždy hovorí pravdu. To znamená, že od žiadneho z nich nemôžete počuť klamstvo aj pravdu v jeho výpovedi. Jeho kamaráti – tí, ktorí tu práve boli (konkrétne Alojz, Bartolomej, Ctibor, Drahomír, Ezechiel, Frederik, Gabriel a Herbert) mu na otázku, koľko má kamarátov, odpovedali takto:
A: Všetci hovoríme pravdu. Máš ich párny počet.
B: Aspoň $1$ z nás ôsmich klame. Máš ich trojciferné číslo.
C: Katka mala dnes na raňajky iba $1$ jogurt a nič iné.
D: Katka mala dnes na raňajky iba $1$ jablko a nič iné.
E: Aspoň $2$ z nás tu klamú. Počet tvojich kamarátov je číslo, ktoré má na mieste stovák $1$.
F: Aspoň $2$ z nás tu hovoria pravdu. Katka raňajkovala iba melón.
G: Katka dnes raňajkovala. Počet tvojich kamarátov je deliteľný $7$.
H: Katka dnes nejedla. Počet tvojich kamarátov nie je deliteľný $9$.
Koľko má Jožko kamarátov

Dino vynásobil svoj vek (menší ako $100$ rokov) tromi a povedal ho Jožkovi. Jožko mal však problémy so sluchom, takže počul číslo odzadu. Číslo, ktoré počul, je Dinov vek pred $2$ rokmi. Koľko rokov bude mať Dino o $2$ roky?

Dino a Jožko sa chcú autom odviezť na kopec za veľkou lúkou. Po ceste však nie sú žiadne čerpacie stanice a auto uvezie len toľko nafty, koľko postačí na jazdu jedného auta do polovice plánovanej cesty. Máme ale k dispozícii Jožkových kamarátov a ich autá (ktoré sú úplne zhodné s tým Jožkovým). Tieto autá parkujú u Jožka v garáži, a z ktoréhokoľvek môžu kedykoľvek preliať obsah (alebo časť) nafty z nádrže do iného auta. Ako teda previesť autami Dina a Jožka za použitia čo najmenej áut? Koľko najmenej áut je na to potrebných? Zdôvodnite, prečo práve tento počet stačí a zároveň, že menej áut Dinovi a Jožkovi nestačí na to, aby sa na kopec odviezli.

Vypočítajte vnútorné uhly rovnoramenného lichobežníka $ABCD$ s dlhšou základňou $AB$, ak viete, že je možné rozdeliť ho dvoma priamkami prechádzajúcimi bodom $A$ na tri rovnoramenné trojuholníky, z ktorých jeden je trojuholník $ABC$.

Súostrovie niekoľkých ostrovov je pospájané mostami. Z každého ostrova vedú najviac $3$ mosty a medzi ľubovoľnými dvoma ostrovami sa vieme presunúť tak, že prejdeme po najviac dvoch mostoch. Koľko najviac ostrovov môže obsahovať toto súostrovie?

Máme rozložené karty v rade vedľa seba. Každá je otočená lícom ($L$) alebo rubom ($R$) nahor. Chceme, aby každá karta bola nakoniec lícom nahor. Otáčať karty však vieme vždy len tak, že si zvolíme štyri susedné karty a všetky ich naraz otočíme na opačnú stranu (ak bola karta lícom nahor, tak je teraz rubom a naopak). Akým spôsobom sa to dá docieliť, ak sú karty na začiatku položené
A) $LRLRRLR$,
B) $RLRRRLRL$?
Ak si myslíte, že to je možné docieliť, tak popíšte postupnosť krokov, ako karty otáčate, ak to možné nie je, tak vysvetlite, prečo (uistite sa, že ste však nezabudli skúsiť všetky možnosti alebo všeobecne ukážte, že to nejde).