
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Matik, 33. ročník - Zimný semester
Vzorové riešenia 1. série nájdeš v časopise Matik-33-2
Vzorové riešenia 2. série nájdeš v časopise Matik-33-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 21. október 2019 20:00:00
1. Šermlok cestou k miestu činu premýšľa nad piatimi zvieratkami, ktoré by mohli byť podozrivé: andulka Adam, bobor Bob, cikáda Cyril, daniel Dano a emu Ema. Vie, že:
- Aspoň jeden z dvojice Adam a Cyril je podozrivý.
- Práve jeden z dvojice Bob a Ema je nevinný.
- V dvojici Bob a Cyril sú buď obidvaja nevinní alebo sú obidvaja podozriví.
- Práve jeden z dvojice Cyril a Dano je nevinný.
- Najviac jeden z dvojice Adam a Ema je nevinný.
2. Šermlok si na zrnku peľu všimol jednu zaujímavú vlastnosť. Je to totiž lichobežník $ABCD$ s rovnobežnými stranami $AB$ a $CD$. Platí v ňom, že $|AB| = 2|CD|$ a $|AD| = |BC|$.Predĺžením polpriamky $DC$ vznikne bod $E$ taký, že $|EC| = |CB| = |BE|$ a predĺžením polpriamky $DA$ bod $F$ taký, že $|AF| = |BA|$. Dokážte, že uhol $|FBC| = 90°$.
3. Na tabuli sú napísané čísla $1$,$2$, ...$150$. V každom kroku si môžeme vybrať ľubovoľné $2$ z nich, zmazať ich a napísať ich súčet alebo nezáporný rozdiel. Môže na tabuli ako posledné zostať číslo $2$? Ak áno, ako máme postupovať, ak nie prečo?
4. V kuchárskej knihe od Mateja Matemakaka sa písalo:
- najväčší spoločný deliteľ gramáže múky a gramáže cukru je $15$,
- najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je $6$,
- súčin gramáže cukru a gramáže citrónovej kôry je $1 800$,
- najmenší spoločný násobok gramáže múky a gramáže cukru je $3 150$.
5. V Starom Lese rastú len bylinky s $5$ a $7$ listami. Keď kanec Vavrínec zbiera suroviny na bylinný mok, tak vždy otrhne celú bylinku a položí ju do košíka. Aký je najväčší počet listov, ktoré sa mu nikdy nepodarí mať v košíku presne? Ako by to vyzeralo, keby v Starom Lese rástli aj $6$-listové bylinky?
6. Šermlokov luster má dva závity na žiarovky a svieti iba vtedy, ak v ňom sú zapojené dve funkčné žiarovky. Šermlok má v šuflíku $5$ funkčných a $5$ nefunkčných žiaroviek. Ako má Šermlok postupovať v skúšaní žiaroviek tak, aby musel vyskúšať čo najmenej párov žiaroviek, kým sa mu podarí luster rozsvietiť. Ukážte aj prečo to na menej nejde.
Vzorové riešenia 1. série nájdeš v časopise Matik-33-2
Vzorové riešenia 2. série nájdeš v časopise Matik-33-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 25. november 2019 20:00:00
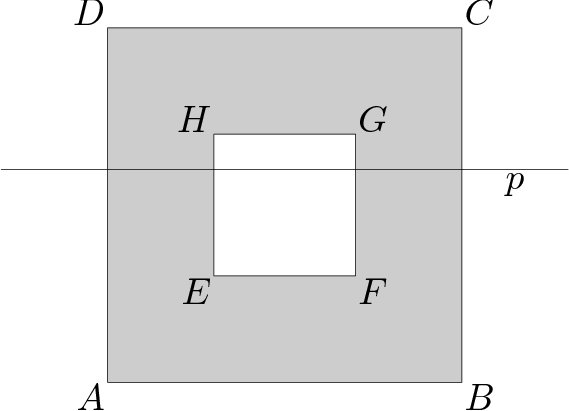
1. Na papieriku bol útvar zložený z $2$ štvorcov a rovnostranného trojuholníka.
Dokážte, že trojuholník AXZ je rovnostranný.

2. Piati medojedi: Ahmed, Bartolomed, Ctimed, Demeder a Elizamed sa hádali o počte džbánov medu, ktoré im ostali v zásobe z pôvodných $100$. Každý medojed buď vždy klame alebo vždy hovorí pravdu. Toto sú výroky jednotlivých medojedov:
- Ahmed: Počet džbánov medu dáva zvyšok $1$ po delení $4$. Hovorím pravdu.
- Bartolomed: Počet džbánov medu je deliteľný $7$ a Demeder je klamár.
- Ctimed: Počet džbánov medu je deliteľný $13$, Demeder a Elizamed nie sú rovnakí.
- Demeder: Počet džbánov medu je deliteľný $3$ a Ahmed je klamár.
- Elizamed: Máme viac ako $40$ džbánov medu, Bartolomed a Demeder sú rovnakí.
3. Zajda a Klára hrajú hru. Najprv Zajda položí na stôl čiernu alebo bielu figúrku. Potom Klára položí čiernu alebo bielu figúrku za tú, ktorá bola na stôl položená naposledy. Takto sa striedajú v pokladaní figúriek na stôl, pričom v rade nemôžu byť $3$ rovnaké figúrky za sebou. Vyhrá tá, ktorá položí do radu deviatu bielu figúrku. Nájdite víťaznú stratégiu pre jednu z nich.
4. Plánik hry, ktorú Zajda a Klára hrali bol pravidelný $9$-uholník. Klára nakreslí na plánik takú priamku, ktorá neprechádza vrcholom plánika. Následne Zajda dokreslí do plánika všetky uhlopriečky, ktoré Klárinu priamku pretínajú. Ukážte, že počet uhlopriečok pretínajúcich Klárinu priamku je párny, bez ohľadu na to, ako ju Klára nakreslí. Čo ak by plánik bol pravidelný $2019$-uholník? Svoju odpoveď zdôvodnite.
5. Majme číslo $n$, ktoré má všetky cifry rôzne a zároveň zoradené od najmenšej po najväčšiu. Zistite aký ciferný súčet môže mať číslo $9n$. Nájdite všetky možnosti.
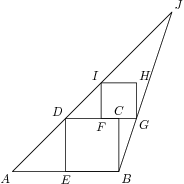
6. Podľa zasadacieho poriadku sú v sále trojuholníkového tvaru umiestnené dva štvorcové stoly ako na obrázku. Platí, že $E$ je stredom $AB$ a zároveň $C$ je stredom $FG$. Koľkokrát je obsah trojuholníkovej sály ABJ väčší ako obsah štvorcového stola BCDE?

Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...