
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Matik, 37. ročník - Letný semester
Vzorové riešenia 1. série nájdeš v časopise Matik-37-5
Vzorové riešenia 2. série nájdeš v časopise Matik-37-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 11. marec 2024 20:00:00
1. Zvýraznené časti zadania boli upresnené 25.2.2024
Artemis a Boreas vymysleli hru s kladnými celými číslami od $1$ do $n$. V hre sa striedajú v ťahoch, a to tak, že v každom ťahu si hráč zoberie jedno z ešte nevybratých čísel. Artemis, ktorá začína, vyhrá, ak bude mať pri sebe na konci dve čísla, ktorých súčin je $n + 1$, inak vyhrá Boreas. Ktorý hráč má vyhrávajúcu stratégiu? (Vyhrávajúca stratégia je postup, podľa ktorého hráč vyhrá bez ohľadu na ťahy súpera.)
Artemis a Boreas vymysleli hru s kladnými celými číslami od $1$ do $n$. V hre sa striedajú v ťahoch, a to tak, že v každom ťahu si hráč zoberie jedno z ešte nevybratých čísel. Artemis, ktorá začína, vyhrá, ak bude mať pri sebe na konci dve čísla, ktorých súčin je $n + 1$, inak vyhrá Boreas. Ktorý hráč má vyhrávajúcu stratégiu? (Vyhrávajúca stratégia je postup, podľa ktorého hráč vyhrá bez ohľadu na ťahy súpera.)
2. Aténa zoslala Pytagorovi úlohu: „Na číselnej osi sú zaznačené body \(x,\) \(2x-2\) a \(3x\) (viete, ktorý bod prislúcha ktorému číslu). Nájdi body 0 a 1.” Ako to mohol Pytagoras spraviť, keď mohol použiť iba kružidlo a pravítko bez mierky?
3. Okolo Herkula stálo v kruhu 17 príšer, z ktorých každá mala iný počet hláv z rozmedzia od 1 do 17. Dokážte, že každé takéto usporiadanie musí mať najmenej jednu skupinu troch susedných príšer, ktoré majú spolu aspoň 27 hláv.
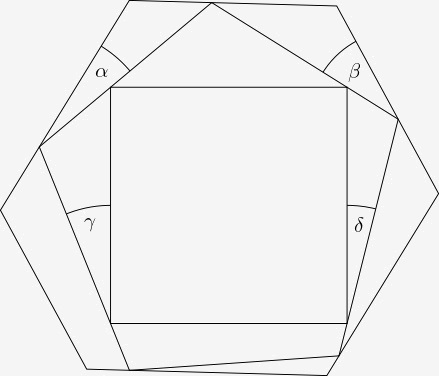
4. Zeus sa rád pozerá na Zem cez okno. Okno má tvar štvorca, ktorého vrcholy ležia na stranách päťuholníka tak, ako na obrázku. Vrcholy päťuholníka zase ležia na stranách šesťuholníka tak, ako na obrázku. Päťuholník má všetky vnútorné uhly rovnakej veľkosti a aj šesťuholník má všetky vnútorné uhly rovnakej veľkosti. Zistite súčet uhlov \(\alpha+\beta+\gamma+\delta\).

5. Počty bohov jednotlivých elementov sú postupne rôzne prvočísla \(l\), \(m\), \(n\), \(t\) také, že \(2\cdot l + 3\cdot m + 5\cdot n + 7\cdot t = 162\) a zároveň \(11\cdot l + 7\cdot m + 5\cdot n + 4\cdot t = 162\). Nájdite všetky možné hodnoty pre \(l\), \(m\), \(n\), \(t\). (Prvočíslo je číslo, ktoré má práve dvoch deliteľov - číslo 1 a seba samé.)
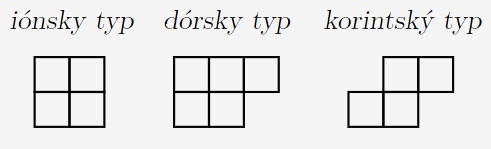
6. Dar bohom mal tvar mozaiky s rozmermi $20 \times 47$. Mozaika sa skladala z ľubovoľne otočených alebo prevrátených dielikov iónskeho, dórskeho a korintského typu nasledujúcich tvarov:
Koľko najmenej dielikov dórskeho typu bolo v mozaike použitých?

Vzorové riešenia 1. série nájdeš v časopise Matik-37-5
Vzorové riešenia 2. série nájdeš v časopise Matik-37-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 8. apríl 2024 20:00:00
1. Héfaistos ukul meč s hrotom v tvare rovnostranného trojuholníka $ABC$. Niekam na jeho stranu $BC$ vypálil bod $D$. Obsah trojuholníka $ABD$ je trikrát väčší ako obsah trojuholníka $ACD$. Rozdiel ich obvodov je $5$ $cm$. Určte veľkosť strany $AB$.
2. Iris priradila siedmim farbám dúhy cifry \(1\) až \(9\), každú najviac raz. Prvej farbe, červenej, priradila cifru \(1\). Všimla si, že súčiny cifier prvých troch farieb, prostredných troch farieb a posledných troch farieb sa rovnajú. Zároveň si všimla, že sedemciferné číslo, ktoré očíslovanie dúhy vytvorilo, je deliteľné jedným z cifier, ktoré nepoužila. Aké cifry priradila Iris jednotlivým farbám dúhy?
3. Zvýraznená časť zadania sa zmenila 28.01.2024
Afrodita napísala na pergamen niekoľko po sebe idúcich kladných celých čísel. Ares roztrhol pergamen na dve časti tak, že:
Afrodita napísala na pergamen niekoľko po sebe idúcich kladných celých čísel. Ares roztrhol pergamen na dve časti tak, že:
- na každej z nich je napísaných niekoľko (aspoň jedno) po sebe idúcich kladných celých čísel,
- na jednej časti je o jedno číslo viac ako na druhej,
- súčty čísel na oboch častiach sa rovnajú.
4. Héra dookola vypĺňala tabuľku $5 \times 4$ tak, že v každej $2 \times 2$ podtabuľke sa nachádzalo každé z jej štyroch obľúbených čísel. Takto dostala niekoľko rôznych vyplnení celej tabuľky $5 \times 4$. Poseidon si po každom vyplnení zapísal súčet všetkých čísel vo vyplnenej tabuľke. Koľko najviac rôznych súčtov mohol mať Poseidon zapísaných?
5. Nebeská záhrada má tvar štvoruholníka $ABCD$, v ktorom platí, že uhol $ACB$ má $90^\circ$, uhol $BAC$ má $35^\circ$ a body $B$ a $D$ sú symetrické (osovo súmerné) podľa priamky prechádzajúcej stredom strany $AB$ a bodom $C$. Aký veľký je uhol $ADC$?
6. V trónnej sále na Olympe bolo 10 bohov. Každý z nich mal od 1 do 100 rokov (vek rátame na celé roky). Dokážte, že spomedzi týchto bohov môžeme vybrať dve neprázdne rovnako staré skupiny (nikto nebude v oboch). Vek skupiny je súčtom vekov jej členov.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...
Ospravedlňujem sa za nepresnosť v minulom komentári, hráči si v každom ťahu berú čísla k sebe a na konci sa pri sebe snažia mať dve so súčinom n+1.
Ahoj, škrtajú čísla až kým na konci neostanú 2 čísla a z týchto 2 sa vyhodnotí, aký majú súčin.
Artemis vyhra ak bude mat na konci dve cisla co maju sucin n+1. To znamena posledne dve nevybrate cisla?
Alebo posledne dve z tych cisel co si vybrala Artemis. Ako sa urcuje kolko je n?
Ahoj, správny termín je 11. marca, do časopisu sa omylom dostal údaj z minulého roka, za čo sa ospravedlňujeme a pokúsime sa to zmeniť aj v časopise na stránke.
Kedy je termín tejto série? V časopise sa píše 27. marca, ale tu na stránke sa píše 11. marca.