Pri vstupe do obchodu odovzdal Jumpy všetky svoje peniaze, ktoré mal pri sebe. Pri odchode dostal dvojnásobok odovzdanej sumy, ale potom ešte zaplatil poplatok $24$ peňazí. Takto chvíľu vchádzal a vychádzal z obchodu, až kým pred vstupom nezistil, že už nemá žiadne peniaze. Koľko peňazí mohol mať Jumpy na začiatku? Nájdite všetky riešenia, ak sa dajú mať len celé peniaze (neexistujú žiadne čiastkové peniaze ako napríklad polovičné).

Obdĺžnikový koláč, ktorý vážil 6 kg, si rozdelili traja ľudia. Najprv koláč rozrezali na dva kusy. Potom jeden z týchto kusov znovu rozrezali na dva kusy. Oba tieto rezy boli rovné. Vznikli takto tri trojuholníky, pričom každý človek si zobral jeden. Jeden z nich mal kúsok ťažký aritmetický priemer hmotností zvyšných dvoch. Koľko vážili kúsky koláča, ak viete, že koláč má všade rovnakú konzistenciu?

Požiarny evakuačný plán v tvare päťuholníka $ABCDE$ má všetky strany rovnako dlhé a uhly pri strane $AB$ sú pravé. Bod $X$ je priesečník úsečiek $AD$ a $BE$. Dokážte, že $|DX| = |BX|$.

Multikulti číslo je také číslo, ktoré má všetky cifry navzájom rôzne. Ku každému multikulti číslu vieme vytvoriť itlukitlum číslo tak, že otočíme poradie jeho cifier (napríklad $1357$ na $7531$ alebo $450$ na $54$). Aké najmenšie a aké najväčšie $5$-ciferné číslo môžeme získať sčítaním multikulti a k nemu príslušného itlukitlum čísel?

Pozdĺž kružnice rulety sú napísané v nejakom poradí všetky prirodzené čísla od $1$ do $2020$ (každé práve raz) tak, že sa pri pohybe po kružnici rulety v smere hodinových ručičiek čísla striedavo zväčšujú a zmenšujú (pre ruletu s číslami od 1 do 4 by mohli byť čísla napísané napríklad v poradí 1, 3, 2, 4). Dokážte, že rozdiel niektorých dvoch po sebe idúcich čísel je deliteľný $2$.

Dokážte, že pre každé kladné celé číslo $n$ platí, že súčin prvých $n$ kladných celých čísel je deliteľný súčtom prvých $n$ kladných celých čísel práve vtedy, keď číslo $n + 1$ nie je nepárne prvočíslo. (To znamená dokázať dve veci. Ak je súčin deliteľný súčtom, tak $n+1$ nie je nepárne prvočíslo a, ak $n+1$ nie je nepárne prvočíslo, tak súčin je deliteľný súčtom).

Mihál nazýva kladné celé číslo mimoňským obľúbeným číslom, ak sa toto číslo po vynásobení svojím ciferným súčtom zväčší $10$-krát. Mihál hľadal mimoňské obľúbené čísla a, keď ich niekoľko našiel, všetky ich medzi sebou vynásobil a vyšlo mu $532$. V spánku však zabudol, ktoré čísla našiel. Ktoré čísla to boli, ak viete, že ich bolo viac ako jedno?

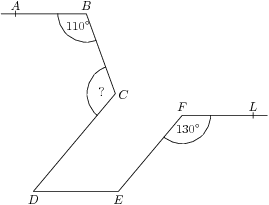
Body $A$, $B$, $C$, $D$, $E$, $F$, $L$ sú ako na obrázku. Veľkosť uhla $ABC$ je $110$ stupňov a veľkosť uhla $EFL$ je $130$ stupňov. Priamka $AB$ je rovnobežná s priamkami $FL$ a $DE$ a zároveň je priamka $CD$ rovnobežná s priamkou $FE$. Aká je veľkosť uhla $BCD$?

Na stole sa nachádza $20$ pokrových žetónov. Špenát Šrac a Chlieb Cézar hrajú hru, v ktorej sa striedajú v ťahoch a Šrac začína. Jeden ťah je odhodenie nejakého počtu žetónov. Odhodiť môžu toľko žetónov, koľko si vyberú, ale stále musia odhodiť aspoň jeden a nikdy nemôžu odhodiť naraz viac ako polovicu žetónov, ktoré budú zostávať na stole. Prehráva jedlo, ktoré už nevie spraviť korektný ťah. Je možné, aby jedno jedlo donútilo to druhé stále prehrať? Ak áno, ako?

Rúčka mala tvar rovnostranného trojuholníka $ABC$, kde na strane $BC$ leží bod $F$. Obsah trojuholníka $ABF$ je trikrát väčší ako obsah trojuholníka $ACF$ a rozdiel obvodov týchto dvoch trojuholníkov je $5$. Určte dĺžku strany trojuholníka $ABC$.

Na obvode hypnotického kruhu je vyznačených šesťdesiat bodov, z ktorých tridsať je zafarbených načerveno, dvadsať je zafarbených namodro a desať je zafarbených nazeleno. Tieto body rozdeľujú kružnicu na šesťdesiat oblúkov. Každému z týchto oblúkov je pridelené číslo podľa farieb jeho koncových bodov: oblúku medzi červeným a zeleným bodmi je priradené číslo $1$, oblúku medzi červeným a modrým bodmi je pridelené číslo $2$ a oblúku medzi modrým a zeleným bodmi je priradené číslo $3$. Oblúk medzi dvoma bodmi rovnakej farby je označený číslom $0$. Aký je najväčší možný súčet všetkých čísel priradených oblúkom?

Strelec cvičil streľbu na pizzu. V strede pizze bolo koliesko klobásy a zvyšok pizze bol pokrytý syrom. Strelec vystrelil dvadsaťkrát. Keď sa trafil do klobásy, získal $30$ bodov, keď sa trafil do časti, kde je syr, získal $18$ bodov, a ak trafil okraj pizze, získal $6$ bodov. Mohlo sa stať aj to, že sa do pizze ani netrafil, a potom nezískal žiaden bod. Na svojom celkovom skóre si všimol, že jeho priemerný bodový zisk za trafenie sa do pizze je $17$ bodov (strely mimo pizze do priemeru nepočítal). Koľko najviac mohol streliť bodov?