
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Matik, 34. ročník - Zimný semester
Vzorové riešenia 1. série nájdeš v časopise Matik-34-2
Vzorové riešenia 2. série nájdeš v časopise Matik-34-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 19. október 2020 20:00:00
1.
V Kamirlande vznikol nový tím FírKe. Na tréningu si hráči nahrávajú disk. O FírKe je známe, že na jednom tréningu nehodia disk menej ako $77$-krát ani viac ako $88$-krát. Tiež platí, že na každom tréningu je počet diskov, ktoré hráči chytia, dvakrát väčší ako počet diskov, ktoré hráči nechytia.
- Koľko najmenej diskov môžu hráči chytiť za tréning?
- Môže tím mať $55$ tréningov, počas ktorých nechytili $1600$ diskov?
2.
Frisbeesti hrajú turnaj vo futbale. Zúčastnili sa tímy Plasto-Kus, FírKe, UpSky a OverLeft a každý tím hral s každým. Za výhru si tím pripíše $3$ body, za remízu $1$ bod a porazený tím nedostane žiadny bod. Poradie sa určilo podľa počtu bodov, v prípade rovnosti bodov rozhoduje vzájomný zápas. V prípade, že zápas skončil remízou, skončil lepšie tím, ktorý dostal menej gólov za celý turnaj. Určte, ako dopadol zápas medzi Plasto-Kusom a FírKe, ak tabuľka na konci turnaja vyzerala takto:
| Poradie | Názov tímu | Skóre | Body |
|---|---|---|---|
| 1. | Plasto-Kus | 7:3 | 5 |
| 2. | FírKe | 4:4 | 4 |
| 3. | UpSky | 1:1 | 4 |
| 4. | OverLeft | 1:5 | 3 |
3. Tréner pripravil pre hráčov na rozcvičku kruhový plánik, ktorý má $12$ stanovísk označených kuželkami očíslovanými od $1$ po $12$. Tréner zakričí číslo $1$ a hráči sa vtedy postavia na stanovisko s číslom $1$. Postupne tréner kričí nasledujúce prirodzené čísla a pri každom čísle sa hráči posunú o jedno stanovisko v kruhu (z dvanásteho idú naspäť na prvé, ale čísla sa ďalej zvyšujú). Vždy, keď je aktuálne zakričané číslo prvočíslo, tak kuželku označujúcu stanovisko vymenia za farebný disk (na stanovisku označenom farebným diskom už nič nemenia). Budú niekedy vymenené všetky kuželky za farebné disky? Ak áno, vysvetlite, ako sa to stane. Ak nie, tak ukážte, ktoré kuželky sa im podarí vymeniť za disk a prečo sa im nepodarí vymeniť tie zvyšné.
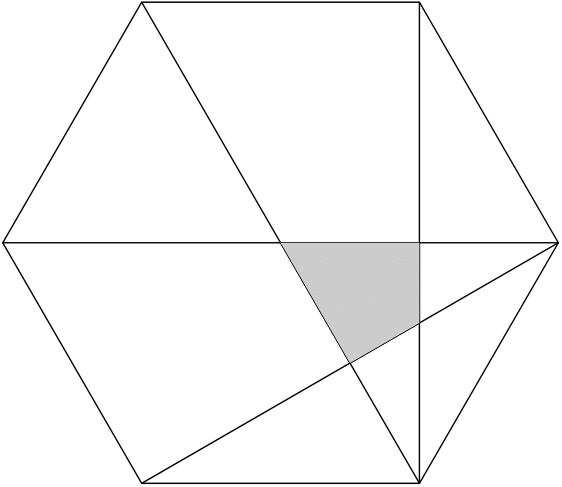
4. Na obrázku máme ihrisko tvorené pravidelným šesťuholníkom s nasledovne vyznačenými uhlopriečkami. Vieme, že jeho vyfarbená časť má obsah $1cm^2$. Aký obsah má celý šesťuholník?

5. Máme $7$ pravých a $7$ falošných diskov, ktoré sú o trochu ľahšie. Máme aj robota, ktorý funguje ako rovnoramenné váhy. Ak mu dáme do dvoch rúk rovnako vážiace disky (alebo skupiny diskov), tak nám to povie. Ak disky (alebo skupiny diskov) v jeho rukách majú rôzne hmotnosti, tak nám povie, v ktorej ruke je ťažší disk (alebo skupina diskov) a zároveň si jeden náhodný disk z ťažšej skupiny vezme ako odmenu. My vyhráme, ak sa nám podarí identifikovať s istotou aspoň jeden pravý disk, ktorý si robot nevzal ako odmenu (nezáleží na tom, o koľko pravých diskov pri tom prídeme). Vieme vyhrať? Ak áno, napíšte ako, ak nie, vysvetlite prečo.
6. Na frisbee kempe bolo niekoľko hráčov a každý z nich nadiktoval trénerom čísla svojich dresov. Každý dres má na sebe nepárne číslo. Trénerka vynásobila všetky dresové čísla dohromady, odčítala od súčinu jednotku a zapísala si polovicu výsledného čísla. Tréner nevie násobiť veľa čísel, a tak radšej od každého dresového čísla odčítal jednotku a potom ho vydelil dvomi. Dostal tak nový zoznam čísel, v ktorom všetky čísla sčítal a zapísal si výsledok. Ukážte, že čísla, ktoré si tréner a trénerka zapísali, majú rovnakú paritu.
Vzorové riešenia 1. série nájdeš v časopise Matik-34-2
Vzorové riešenia 2. série nájdeš v časopise Matik-34-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 23. november 2020 20:00:00
1. Po vytrvalom trénovaní počas leta si chcel tréner svojich hráčov odvážiť, aby zistil, aký pokrok urobili. Stálo pred ním $11$ hráčov, o ktorých vedel, že schudli nasledovne:
- všetci hráči schudli dokopy $40kg$,
- hráči na párnych pozíciách schudli dokopy $16,5kg$,
- hráči na pozíciách deliteľných 3 schudli dokopy $12,5kg$,
- súčet hmotností, ktoré schudli dvaja krajní a traja prostrední hráči je dokopy $19kg$.
2. Na turnaj prišlo $35$ hráčov vrátane teba. Medzi niektorými z vás už existujú vzájomné priateľstvá a zároveň každý hráč má aspoň $17$ kamarátov. Skamarátiť sa s nejakým hráčom je možné iba vtedy, ak sa s ním kamaráti už niektorý z tvojich doterajších kamarátov. Ukáž, že sa vieš skamarátiť so všetkými hráčmi.
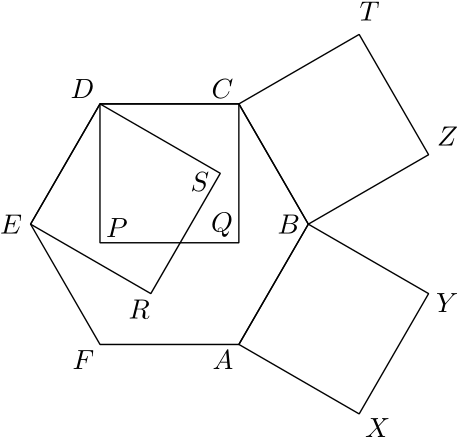
3. Na obrázku je nakreslený návrh nových kraťasov. Tie sú tvorené pravidelným šesťuholníkom $ABCDEF$ a dvoma štvorcami $BAXY$ a $CBZT$. Na kraťasoch sú dva vzory $CDPQ$ a $DERS$, ktoré sú tiež štvorce. Ukážte, že $|PS| = |YZ|$.

4. Na frisbee campe sú pravdovravci a klamári. Všetci pravdovravci hovoria vždy pravdu a všetci klamári vždy klamú. Niektorí pravdovravci sa rozhodli hrať HotBox, podobne niektorí klamári začali hrať discgolf. Ľudia na campe sa združili do rôznych tímov, pričom hráč môže patriť do viacerých tímov. Tímy, ktoré vznikli na frisbee campe, spĺňajú nasledujúce $4$ podmienky:
- Všetci pravdovravci, ktorí hrajú HotBox, tvoria tím.
- Všetci klamári, ktorí hrajú discgolf, tvoria tím.
- Pre každý tím $T$ platí, že tí hráči, ktorí nie sú v tíme $T$, tvoria tiež tím.
- Ku každému tímu $T$ existuje aspoň jeden hráč, ktorý o sebe prehlasuje, že je členom tímu $T$ (jeho tvrdenie nemusí byť pravdivé, môže to byť klamár).
5. Nedávno si si zmenil číslo svojho dresu. Toto číslo $n$ má po delení $3$ zvyšok $2$. Ukáž, že potom existuje prvočíslo $p$, ktoré delí $n$ a tiež má po delení $3$ zvyšok $2$.
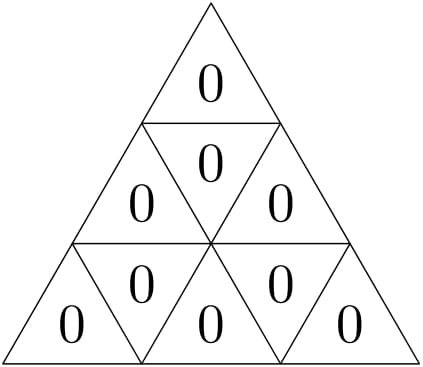
6. Po dlhom dni plnom zápasov sa Marco rozhodol, že si zahrá hru. Nakreslil si rovnostranný trojuholník, ktorý rozdelil na $9$ menších trojuholníkov. V každom malom trojuholníku je napísané číslo $0$. Hra spočíva v tom, že Marco si v každom ťahu vyberie $2$ trojuholníky, ktoré majú spoločnú stranu, a pričíta alebo odčíta rovnaké celé číslo od oboch čísel, ktoré sú v trojuholníkoch napísané. Po nejakom čase si uvedomí, že čísla napísané na $9$ trojuholníkoch sú v nejakom poradí $n$, $n+1$,..., $n+8$, kde $n$ je nezáporné celé číslo. Ukážte, že hodnota $n$ môže byť len $0$ alebo $2$ (nemusíte ukazovať, že to pre tieto hodnoty môže nastať).

Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...
Ahoj! Zadanie priamo nehovorí, že by na každom tréningu hodili rovnako veľa diskov.
Dobrý deň, myslí sa to tak, že na každom treningu hodia rovnaký počet diskov, alebo môže byť rôzný ke´d sa neporušuju zadania ulohy? Ďakujem
Ahoj! Myslí sa práve 1600 diskov.
Dobrý večer, myslí sa to ako PRESNE 1600 diskov? Alebo ich mohli nechytiť aj viac? Ďakujem