Na túru prišlo aspoň $5$ detí (aspoň $1$ chlapec a aspoň $1$ dievča). Niektorí chlapci sa s niektorými dievčatami zvítali objatím. Všetky dvojice, ktoré sa neobjali, si iba podali ruky. Môžeme ľudí rozdeliť do dvoch skupín tak, aby ani v jednej skupine neboli dve deti, ktoré si spolu podali ruku? Ak áno, ako? Ak nie, prečo?

Tri horolezkyne Adel, Bia a Lujza rady lezú. Dve stále lezú a jedna ich istí. Tá, ktorá z dvojice vylezie na kopec ako prvá, na ďalšom kopci istí a tá, čo istila, ide liezť. Po vylezení všetkých kopcov zistili, že Adel liezla dokopy $12$-krát, Bia liezla dokopy $21$-krát a Lujza $8$-krát istila. Ktorá z horolezkýň vyliezla ako prvá na šiesty kopec?

Máme stan so štvorcovým pôdorysom $ABCD$. Doň si Mihál položil jednu topánku (označme ju $P$) tak, aby trojuholník $ABP$ bol rovnostranný. Druhú topánku (označme ju $Q$) si však zabudol pred stanom tak, že trojuholník $ADQ$ je rovnostranný. Dokážte, že body $P$, $Q$ a $C$ ležia na jednej priamke.

Dano má konzervu tvaru rovnobežníka $ABCD$. V akom pomere rozdeľuje priamka prechádzajúca vrcholom $A$ a stredom strany $CD$ uhlopriečku $BD$?

Dano a Mihál na túre hrali nasledovnú hru: Mihál povedal kladné celé číslo a Dano ho musel zapísať ako súčet niekoľko po sebe idúcich kladných celých čísel. Ak sa mu to podarilo, vyhral. Pri akých číslach vie Dano vyhrať?

Spišo bol už hladný a tak sa rozhodol, že sa posilní čokoládou. Čokoláda má tvar štvorcovej mriežky s rozmermi $k\times k$. Spišo z nej začne vyjedať po jednom políčku. Nájdite najmenšie prirodzené číslo $n$ také, že ak Spišo zje z čokolády $n$ políčok, tak budú s istotou existovať $3$ zjedené políčka, ktorých stredy tvoria pravouhlý trojuholník, ktorého odvesny sú rovnobežné so stranami štvorcovej čokolády.

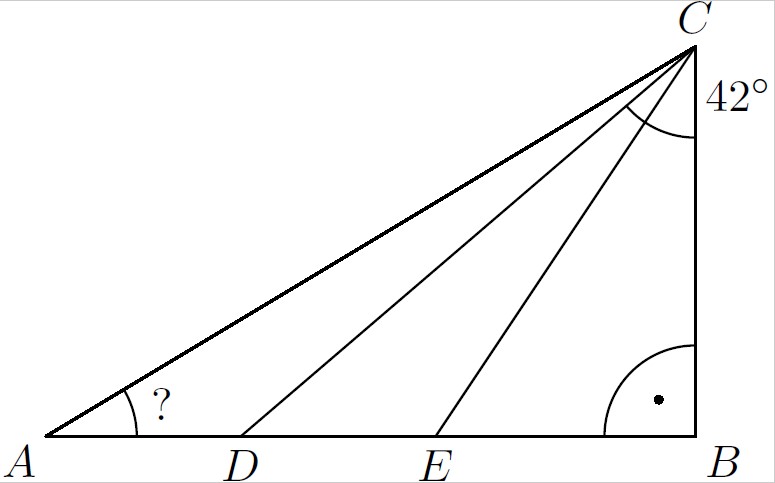
Na mape sú mestá $A$, $B$, $C$, $D$ a $E$. Dorot sa chce zorientovať pomocou tejto mapy, a preto chce nájsť veľkosť uhla $BAC$, ak vie že priamka $CD$ rozdeľuje uhol $ACE$ na polovicu, $|AE| = |EC|$, veľkosť uhla $DCB$ je $42$ stupňov a uhol pri vrchole $B$ je pravý.

Na túre boli štyri dievčatá Kel, Lujza, Maxi a Naťa a dvaja chlapci Dano a Erik. Počas túry si vymenili vaky tak, že každý mal po výmene (ale aj pred ňou) práve jeden vak. Boli povedané nasledujúce pravdivé výroky:

• Kel: „Môj vak má Dano“,
• Lujza: „Môj vak má ten, koho vak má Erik“,
• Maxi: „Môj vak má ten, koho vak má ten, koho vak má Erik“,
• Naťa: „Môj vak má ten, koho vak má ten, koho vak má ten, koho vak mám ja“.

Juro sa chcel ísť pozrieť na vrch vyhliadkovej veže, ktorá má $1000$ poschodí. Povedal si, že zvládne vyšliapať najviac prvých $200$ poschodí (prízemie berieme ako nulté poschodie). Zvyšok cesty chce ísť výťahom. Výťah má tlačidlá $+1$ poschodie, $+3$ poschodia, $+9$ poschodí, $+27$ poschodí, $+81$ poschodí, pričom Juro sa chce dostať na vrch veže na čo najmenší počet stlačení tlačidiel. Koľko najviac stlačení Juro bude potrebovať na to, aby výťah dostal na $1000$. poschodie potom, čo doň na niektorom poschodí nastúpi?

Paťo si nesie na túre cukríky v dvoch balíčkoch. V prvom je ich $m$ a v druhom $n$, pričom $m$ a $n$ sú kladné celé čísla. Paťo vie buď zobrať z oboch balíčkov rovnaký počet cukríkov a zjesť ich, alebo vie zdvojnásobiť počet cukríkov v ľubovoľnom z balíčkov. Pre aké hodnoty $m$ a $n$ vie Paťo po konečnom počte krokov vyprázdniť oba balíčky s cukríkmi? A čo v prípade, ze by nemohol počet cukríkov zdvojnásobovať, ale mohol by ich strojnásobovať?

Na stôl v altánku Jano nakreslil priamku a na nej vyznačil v tomto poradí body $A$, $B$, $C$ a $D$ tak, že $|AB|=|CD|$. Nad priamku potom dvakrát pichol nožíkom. Vzniknuté body označil $P$ a $Q$. Platí, že trojuholníky $ABP$ a $BDQ$ sú rovnostranné. Dokážte, že trojuholník $CPQ$ je rovnostranný. Zadanie bolo upravené.

V Košiciach sú tri turistické kluby, z ktorých má každý $2021$ členov. Zároveň platí, že nikto nie je členom viacerých turistických klubov. Tiež vieme, že každý turista má medzi turistami z iných klubov dokopy aspoň $2022$ kamarátov. Dokážte, že existuje trojica turistov z rôznych klubov, v rámci ktorej sa priatelí každý s každým.