
Pozrite sa na
Správa účtu

Zadania seminára Matik, 38. ročník - Zimný semester
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 21. október 2024 20:00:00
1. Aradin a Tymiána hrajú hru, v ktorej je $5$ kariet s číslami od $1$ do $5$, každé práve raz. Každý z nich si potiahne jednu kartu s číslom, ktorú vidí len on sám. Po potiahnutí kariet prebehla nasledujúca diskusia:
- Tymiána: „Neviem, koho číslo je väčšie.“
- Aradin: „Ani ja neviem, koho číslo je väčšie.“
- Tymiána: „Tak potom už viem, že tvoje číslo je väčšie.“
2. Abum si z koberca vyrezal štvorec \(ABCD\) so stranou dlhou \(\SI{8}{cm}\). Stred strany \(AB\) si označil ako \(E\) a následne zo štvorca odstrihol trojuholník \(BCE\). V novovzniknutom útvare si označil stred strany \(CE\) ako \(F\) a z útvaru odstrihol trojuholník \(CDF\). Napokon si označil stred strany \(DF\) ako \(G\) a z útvaru odstrihol trojuholník \(EFG\). Vypočítajte obsah výsledného útvaru, ktorý Abum získal.
3. Obchodník na trhu predáva vajcia v košíkoch. Na predaj sú košíky s vajciami v počtoch od $1$ do $10$ a na začiatku dňa je na stole práve jeden košík z každého počtu. Každé vajce je buď bielej, alebo hnedej farby (v jednom košíku však môžu byť vajcia oboch farieb). Na trh postupne prišli traja zákazníci a každý z nich si kúpil práve $1$ košík, pričom:
- po nákupe prvého zákazníka ostalo na stole $5$-krát viac bielych ako hnedých vajec,
- po nákupe druhého zákazníka ostalo na stole $6$-krát viac bielych ako hnedých vajec,
- po nákupe tretieho zákazníka ostalo na stole opäť $5$-krát viac bielych ako hnedých vajec.
4. Na poličku s mriežkou \(8 \times 8\) ukladáme magické lampy tvaru \(1 \times 2\) tak, aby platilo, že ak je nejaké políčko zakryté lampou, tak políčko vpravo od neho a políčko pod ním nie je zakryté inou lampou. Koľko najviac lámp môžeme takto na mriežku poličky položiť?
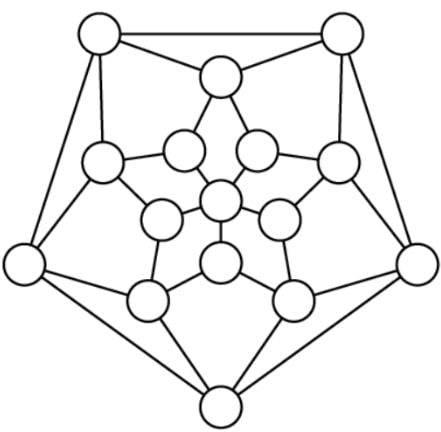
5. Na každom vrchole pohoria stojí človek s nejakým počtom lietajúcich kobercov. Kobercov je spolu $3360$. Všetci sa naraz zbavia kobercov tak, že rozpošlú svoje koberce svojim susedom, každému rovnako veľa (čiary v obrázku znázorňujú susednosti vrcholov). Po výmene kobercov má každý človek rovnako veľa kobercov ako na začiatku. Koľko kobercov môže mať človek v strede pohoria? Nájdite všetky možnosti.

6. Na plachte používanej na trhovisku tvaru mnohouholníka \(A_1A_2 \dots A_n\) ofarbíme každú stranu a uhlopriečku načerveno alebo namodro tak, že strany \(A_1A_2\) a \(A_2A_3\) budú červené a strana \(A_3A_4\) a všetky uhlopriečky vedúce z vrcholu \(A_3\) budú modré. Navyše platí, že pri každom takomto ofarbení existuje aspoň $49$ dvojfarebných trojuholníkov, pričom existuje aj ofarbenie, pri ktorom ich je práve $49$. Nájdite všetky možné hodnoty \(n\).
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 18. november 2024 20:00:00
1. Na gobelíne tvaru štvoruholníka \(ABCD\) existuje na strane \(AD\) bod \(M\) taký, že trojuholníkové výšivky \(MCD\) a \(MAB\) sú rovnostranné. Dokážte, že uhlopriečky tohto gobelínu sú rovnako dlhé. Úlohu neriešte meraním.
2. Na stene sú napísané čísla \(1,2,3,\dots, 673\). Aradin a Bafar striedavo zmazávajú čísla, až kým na tabuli neostanú len $2$ čísla. Aradin začína. Ak je súčet posledných dvoch čísel deliteľný $8$, vyhráva Aradin, ak nie, vyhráva Bafar. Pre ktorého z hráčov existuje výherná stratégia? Výherná stratégia je postup, podľa ktorého hráč vyhrá bez ohľadu na ťahy súpera.
3. Magická Anábia sa vyznačuje tým, že každý jej obyvateľ má priradené kladné celé číslo. Zároveň každý pozná len svoje číslo a nepozná číslo ostatných. Traja kamaráti Aradin, Tymiána a Džinus išli jedného dňa za vševedomým zrkadlom, ktoré im prezradilo, že súčet ich čísel je $100$. Potom postupne povedali:
- Tymiána: „Ja a Džinus nemáme rovnaké čísla.“
- Aradin: „To som už vedel.“
- Tymiána: „Tak teraz viem aj to, že všetci máme rôzne čísla.“
- Džinus: „Tak ja už poznám číslo každého z nás.“
4. Tymiána si do piesku napísala tri rôzne prirodzené čísla a označila si ich \(a\), \(b\), \(c\). Následne zistila, že všetky tieto $3$ čísla sú prvočísla a aj všetky $3$ rozdiely medzi týmito číslami po dvojiciach sú prvočísla. Aké čísla mohla Tymiána napísať na tabuľu? Nájdite všetky možnosti.
5. Do každého riadku tabuľky \(9 \times 9\) vyšitej na koberci zapíšeme jednu z cifier od $1$ do $9$ v poradí tak, že v prvom stĺpci začneme ľubovoľnou cifrou a potom do stĺpca napravo píšeme stále číslicu o $1$ väčšiu, ale po $9$ píšeme $1$ (napr. v riadku môžu byť zaradom čísla $7$, $8$, $9$, $1$, $2$, $3$, $4$, $5$, $6$). Tabuľka je úžasná, ak v každom riadku, v každom stĺpci aj na každej najdlhšej diagonále (z rohu do rohu tabuľky) je napísané $9$-ciferné číslo, ktoré je deliteľné číslom $9$. Koľko rôznych úžasných tabuliek existuje?
6. Lichobežníková šatka \(ABCD\) je taká, že \(|AB| = \SI{8}{cm}\), \(|CD| = \SI{4}{cm}\) a súčet veľkostí uhlov \(DAB\) a \(CBA\) je $90°$. Zistite, akú vzdialenosť môžu mať medzi sebou stredy základní \(AB\) a \(CD\). Úlohu neriešte meraním.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!
 Prosím čakajte ...
Prosím čakajte ...