
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Matik, 30. ročník - Zimný semester
Vzorové riešenia 1. série nájdeš v časopise Matik-30-2
Vzorové riešenia 2. série nájdeš v časopise Matik-30-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 17. október 2016 20:00:00
1. Jančiho svedomie tvorí 100 skutkov vykonaných v istom poradí, o ktorých bolo potrebné rozhodnúť, či sú dobré alebo zlé. Vnútorný hlas mu našepkal, že z každých piatich za sebou vykonaných skutkov sú práve tri skutky zlé. Janči si ešte uvedomil, že prvý a posledný skutok každého človeka je dobrý.
- Určte koľkokrát Janči spáchal nejaký zlý skutok.
- Rozhodnite, či bol šiesty Jančiho skutok dobrý alebo zlý.
- Vysvetlite, ako by ste vedeli pre ľubovoľný z týchto 100 skutkov správne určiť, či bol dobrý alebo zlý.
- Určte koľkokrát Janči spáchal nejaký zlý skutok.
- Rozhodnite, či bol šiesty Jančiho skutok dobrý alebo zlý.
- Vysvetlite, ako by ste vedeli pre ľubovoľný z týchto 100 skutkov správne určiť, či bol dobrý alebo zlý.
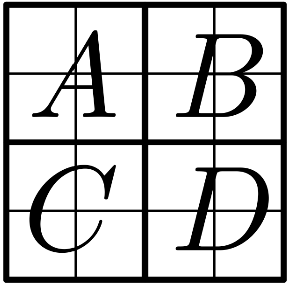
2. Jančiho známi žijú v oblasti, ktorá má podobu mriežky $4\times4$ (viď obrázok). Každú hodinu od 17. do 32. má v pláne navštíviť jedného z nich. Chce si to naplánovať tak, že priradí každému známemu (políčku mriežky $4\times4$) jednu z týchto hodín (prirodzených čísel) tak, aby v každej štvrti (štvrtine mriežky, štvorci $2\times2$ $A$, $B$, $C$ alebo $D$) bol súčin hodín návštev deliteľný číslom 16. Je pre Jančiho možné takýto plán zostaviť? Svoje riešenie zdôvodnite.

3. Keď k trpaslíkovi Janči podišiel, videl, že má $500$ zlatiek. Vždy, keď trpaslíkom potrasie, vysype sa z neho $300$ zlatiek, ak toľko ešte má. Ak nie, nevypadne z neho ani minca. Okrem toho mu Janči vie vložiť do úst práve 198 zlatiek naraz, ktoré trpaslík pridá k tým, čo v sebe má. Akej najväčšej hotovosti sa vie Janči zmocniť, pokiaľ na začiatku nemal ani deravý groš (a ani zlatku)? Trpaslíka môže kŕmiť a triasť koľkokrát chce a v ľubovoľnom poradí.
4. Na zvitku bol narysovaný štvorec $ABCD$ a obdĺžnik $DEFG$, kde bod $E$ ležal na polpriamke opačnej k $BA$ a bod $C$ bol bodom úsečky $FG$. Dokážte, že pri ľubovoľnej polohe bodu $E$ je obsah obdĺžnika $DEFG$ rovný obsahu štvorca $ABCD$.
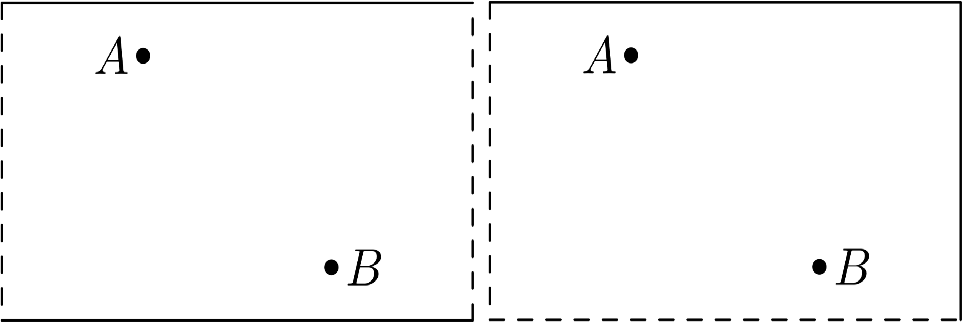
5. Najprv si Janči potrénuje lietanie. Od Zmokovho stromu (bod $A$) chce preletieť k novovytunelovanému tunelu (čiarkovaná čiara), odtiaľ k rozpadnutému diaľničnému úseku Nižná Váha – Vyšná Váha (druhá čiarkovaná čiara) a napokon domov (bod $B$). Nájdite najkratšiu trasu Jančiho letu pre situáciu na obrázku naľavo a pre situáciu na obrázku napravo.

6. Na jednom políčku šachovnice $8\times8$ leží čierny kameň a na ostatných políčkach biele. V jednom kroku môžeme zmeniť na opačné (čierne na biele a biele na čierne) súčasne všetky štyri kamene v ktoromkoľvek štvorci $2\times2$ na šachovnici. Zistite, či po určitom počte krokov môže byť na šachovnici rovnaký počet kameňov oboch farieb.
Vzorové riešenia 1. série nájdeš v časopise Matik-30-2
Vzorové riešenia 2. série nájdeš v časopise Matik-30-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 28. november 2016 20:00:00
1. Janči na úteku si chce urobiť prieskum okolia. Má v záujme prejsť si niekoľko strategických bodov. Vychádza z brlohu potkanieho šéfa a chce navštíviť hrad, družstevnú sýpku, palác, most a nábrežie a zakončiť svoje putovanie opäť v brlohu. Časy prechodu medzi jednotlivými miestami sú:
Nakreslite obrázok a navrhnite plán najkratšej možnej cesty pre Jančiho.
| brloh - sýpka: $2,4$ | sýpka - nábrežie: $1,0$ | hrad - palác: $3,0$ |
| brloh - most: $5,0$ | sýpka - palác: $3,6$ | hrad - most: $4,6$ |
| brloh - nábrežie: $2,8$ | sýpka - hrad: $3,8$ | nábrežie - palác: $3,0$ |
| brloh - palác: $3,4$ | sýpka - most: $3,6$ | nábrežie - most: $1,6$ |
| brloh - hrad: $2,4$ | hrad - nábrežie: $3,2$ | most - palác: $3,2$ |
2. Janči sa ponoril do oparu katakomb a ocitol sa v hlavnej chodbe. Z nej viedlo mnoho bočných chodieb. Nad každým z východov bol osadený kameň s číslom. Janči si všimol, že súčet každých troch po sebe idúcich čísel je $20$ alebo $22$. Striedajú sa postupne v poradí $20$, $20$, $22$, $22$, $20$, $20$, $22$, ... Nad prvým východom bolo číslo $9$, nad deviatym $7$. Aký je súčet čísel prvých $100$ východov?
3. Ukážte, že $6$ trojuholníkov, ktoré vznikli rozdelením trojuholníka tromi ťažnicami, má rovnaké obsahy. Ťažnice sa vždy pretínajú v jednom bode, ktorý nazývame ťažisko.
4. Na stole ležala kocka a po poslednom hode vyzerala takto: V jej vrcholoch sa vznášali čísla od $1$ po $8$ (každé práve raz). Na každej stene kocky bol vyrytý súčet čísel, ktoré sa nachádzali vo vrcholoch príslušnej steny. Bolo zaujímavé, že všetky súčty na stenách, ktoré Janči videl (tých stien bolo päť), boli prvočísla a neboli medzi nimi žiadne dve rovnaké. Aké číslo bolo na šiestej stene kocky?
5. Chceli, nech Janči dokáže, že ak si ľubovoľne zvolíme $55$ rôznych celých čísel od $1$ do $100$ vrátane, budú medzi nimi dve, ktorých rozdiel je $9$, dve, ktorých rozdiel je $10$, dve, ktorých rozdiel je $12$ a dve, ktorých rozdiel je $13$. Prekvapujúco sa mocní nevedeli zmocniť vždy takých dvoch čísel, ktorých rozdiel je $11$, takže treba ukázať, že také tam byť nemusia.
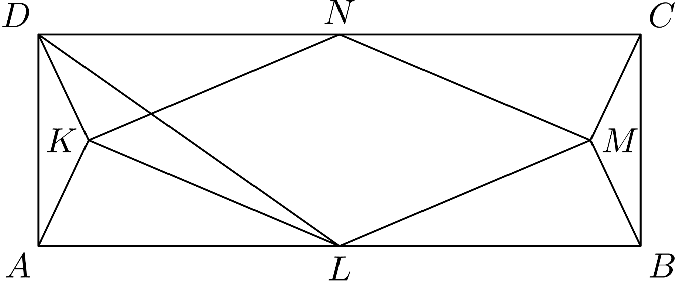
6. V obdĺžniku $ABCD$ sa nachádzajú body $K$, $L$, $M$ a $N$ ako na obrázku. Daný útvar na obrázku je osovo súmerný podľa osí $KM$ aj $NL$. Pritom platí, že $|\angle ADK| = |\angle CDL| = 30^\circ$. Akú časť plochy obdĺžnika $ABCD$ zaberá kosoštvorec $KLMN$?

Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...