
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Matik, 31. ročník - Letný semester
Vzorové riešenia 1. série nájdeš v časopise Matik-31-5
Vzorové riešenia 2. série nájdeš v časopise Matik-31-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 26. marec 2018 20:00:00
1. Máme $2$ krabice. V každej je $10$ balíčkov korenín. Každý balíček môže obsahovať červené, zelené alebo žlté korenie, ale vždy jednofarebné. V jednej krabici je aspoň $7$ balíčkov žltého korenia a v druhej aspoň $4$ balíčky červeného. Dokopy je dvakrát viac žltých ako zelených balíčkov. Ukážte, že počet červených balíčkov sa rovná buď počtu žltých, alebo zelených balíčkov.
2. Okolo okrúhleho stola sedelo desať zamestnancov. Poznáme z nich pána Kotletkina, ktorý mal $26$ rokov a pána Čajíkovského, ktorý mal $33$. Zaujímalo by ma, či môže byť vek každého zamestnanca sediaceho okolo stola aritmetickým priemerom vekov dvoch kolegov sediacich priamo po jeho ľavici a po pravici. Ak môže, tak nájdite príklad, ako by mohli sedieť zamestnanci okolo stola a napíšte ich veky. Ak nemôže, tak odôvodnite prečo. Veky zamestnancov sú celé čísla.
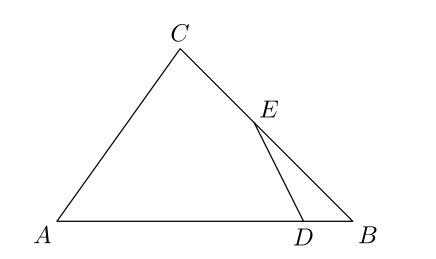
3. Reštaurácia mala tvar trojuholníka. Určte obsahy reštauračnej časti, štvoruholník $ADEC$, a kuchyne, trojuholník $DBE$, ak obsah trojuholníka $ABC$ je $42$ a $|AD|:|DB|=5:1$ a $|BE|:|EC|=4:3$

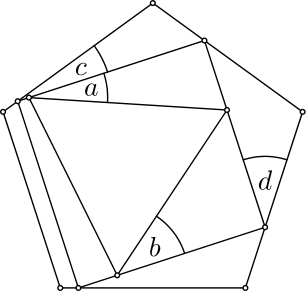
4. Na obrázku je stôl tvaru štvorca, ktorého vrcholy sa dotýkajú strán pravidelného päťuholníka. Na štvorcovom stole je položený trojuholníkový obrus tak, že vrcholy tohto rovnostranného trojuholníka sa dotýkajú strán stola. Zistite hodnotu súčtu vyznačených uhlov $a+b+c+d$. Žiaden z uhlov však nemerajte, keďže rysovanie nie je presné, ale súčet uhlov na ktorý sa pýtame vypočítajte.

5. Do taniera s mriežkou $4\times 4$ chceme podávať niekoľko kusov koláčov. Vieme, že v noci príde pán Oven a zje koláče v dvoch riadkoch a dvoch stĺpcoch. Koľko najmenej koláčov musíme podávať na tanier, aby po nočnom nájazde pána Ovena ostal ráno aspoň jeden kus koláča na tanieri pre pani Ovenovú?
6. Majme sedem celých čísel takých, že súčet ľubovoľných šiestich z nich je deliteľný piatimi. Dokážte, že potom každé z čísel musí byť deliteľné piatimi.
Vzorové riešenia 1. série nájdeš v časopise Matik-31-5
Vzorové riešenia 2. série nájdeš v časopise Matik-31-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 30. apríl 2018 20:00:00
1. Daný je rovnoramenný trojuholník $ABC$ so základňou $AB$ dĺžky $12$ cm a výškou o polovicu menšou. Body $K$, $L$ ležia v tretine strán $AC$ a $BC$ bližšie k vrcholom $A$ a $B$. Vypočítajte obsah obdĺžnika $GFLK$, ak $F$, $G$ ležia na strane $AB$.
2. Obrazy sú označené číslami $1, 2, \dotsc, 25$ a sú rozmiestnené do piatich riadkov a piatich stĺpcov štvorcovej mriežky $5\times 5$. Uvažujme súčty čísel v každom riadku a každom stĺpci. Medzi týmito desiatimi hodnotami sú párne čísla (párne súčty) a nepárne čísla (nepárne súčty). Označme $p$ súčet všetkých párnych súčtov a $n$ súčet všetkých nepárnych súčtov. Môžu byť čísla $1, 2, \dotsc, 25$ rozmiestnené do mriežky tak, aby platilo $p=n$?
3. Hra vyzerala nasledovne: Guličky usporiadali do troch skupín o počte $11$, $12$ a $13$. Bet a Moc mali za úlohu ich všetky postupne zobrať a hrali hru na ťahy. Ťah vyzeral tak, že ten, kto bol na rade, musel zobrať dve guličky, každú z inej skupiny. Kto nemohol zahrať takto predpísaný ťah, prehral. Nájdite výhernú stratégiu pre niektorého z hráčov. (Výhernou stratégiou rozumieme návod, ako má hráč hrať, aby vždy vyhral, nech ten druhý hrá akokoľvek.)
4. Babka Eva Rosina a jej vnuk Moc majú narodeniny v rovnaký deň. Pri šiestich posebe idúcich oslavách narodenín bol babkin vek vždy deliteľný vekom Moca. Koľké narodeniny oslavovala babka na poslednej z týchto šiestich osláv? Babka nemá viac ako $100$ rokov a veky sú celé čísla. Nezabudnite nájsť všetky možnosti a odôvodniť, že iné neexistujú.
5. Na papieriku stálo: usporiadaný rad čísel obsahuje čísla $1$, $2$, $3$, $4$, $5$, $6$, $7$ v nejakom poradí. Každé číslo tohto radu, okrem prvého, delí súčet všetkých predchádzajúcich čísel znížený o $1$. Ktoré čísla môžu byť posledné v rade, ak je prvým číslom sedmička?
6. Štvorec $ABCD$ má veľkosť strany $6$ cm. Stredy strán $AB$ a $AD$ označme ako body $E$ a $F$. Úsečky $CF$ a $DE$ rozdelia štvorec na štyri útvary. Vypočítajte obsahy týchto útvarov.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...
Na to máme vyhradený e-mail, ktorý nájdeš v pravidlách. Avšak musíš rátať s bodovou stratou, nakoľko riešenie posielaš v podstate 24 hodín po termíne.
Ďakujem Jakub inak ako môžem poslať riešenia ak ešte štyri dni po termíne sa to dá???
Ahoj Jakub,
ako iste vieš (keďže si čítal pravidlá), na odovzdávanie úloh neslúžia komentáre. Tu sa môžeš pýtať na otázky ohľadom zadania, no určite by si nemal ostatným ukazovať svoje riešenie úlohy. Z tohto dôvodu boli tvoje komentáre zmazané.
Ak máš záujem o odovzdanie úloh, môžeš tak urobiť iba spôsobmi, ktoré sú uvedené v pravidlách (uvedomujem si, že to nemôžeš odovzdať cez stránku, nakoľko termín série bol včera).