Zo všetkých piatich chlapcov iba jeden vie, kde našli drakkar. Avšak ani pri výsluchu nevravia všetci pravdu. Vyplašení pohľadom na nablýskanú čepeľ každý utrúsil jednu vetu. V poradí títo piati povedali:

1. Ja som ten, kto vie, kde bol drakkar.
2. Ten, kto vie, kde bol drakkar, ešte nebol vypočutý.
3. Ja nie som ten, čo vie, kde bol drakkar.
4. Ten, kto vie, kde bol drakkar, prehovoril ako druhý v poradí.
5. Jeden z prvých dvoch vie, kde sa drakkar našiel.

V pretláčacom turnaji sú štyria piráti a každý sa pretláča s každým práve raz. Pirát získa za výhru $3$ body, za remízu $1$ bod a za prehru $0$ bodov. Aký je najmenší počet bodov, ktorý môže mať pirát na konci turnaja, pričom bude mať stále viac bodov ako všetci ostatní piráti? Ukážte, ako vie tento počet bodov získať a nezabudnite odôvodniť, prečo menej bodov už mať určite nemôže.

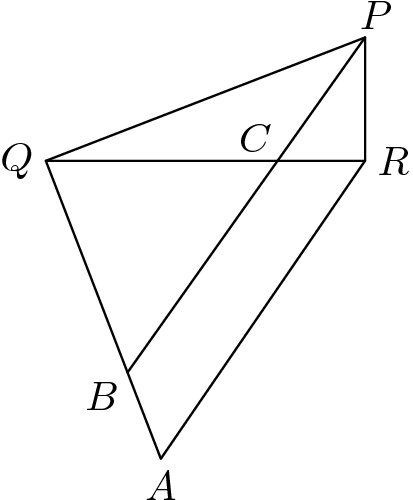
Obrazec mal nasledujúci tvar ako na obrázku a Jack, ktorý mal dobré matematické vzdelanie vedel, že o ňom platí toto: $|QR|=|QA|$, uhly $AQP$ a $PRQ$ sú pravé a $PC$ je os uhla $QPR$. Ukážte, že úsečka $BC$ je rovnobežná s úsečkou $AR$ a že trojuholník $QBC$ je rovnoramenný.

Je možné zdolať dvestohlavého draka mečom z kráľovskej zbrojnice, ak ho môžeme použiť nasledovnými tromi spôsobmi? Sekom sa dá naraz odseknúť drakovi $48$ hláv, ale $33$ nových mu narastie. Šmykom sa dá odťať $21$ hláv a žiadna nová nenarastie. Fikom sa odsekne len jedna hlava a ešte narastie $7$ nových. Každý manéver sa dá použiť iba vtedy, keď má drak dostatočný počet hláv. Keď drak príde o všetky svoje hlavy, nové mu už nenarastú.Svoje riešenie poriadne odôvodnite.

Na poskladanom papieri stálo: Heslo je prirodzené číslo, ktoré neobsahuje nulu. Keď k tomuto heslu pripočítam všetky ďalšie rôzne čísla, ktoré môžu vzniknúť prehádzaním číslic môjho hesla, dostanem $4218$. Jack mužom dychtiacim po odpovedi chcel povedať aspoň aké najmenšie a aké najväčšie číslo mohol kuchár použiť. Aké to boli?

Na začiatku sú na papieri napísané čísla $1$, $2$, $\dots$, $n$. V každom ťahu si môžeme vybrať dve ľubovoľné čísla, ktorých aritmetický priemer je celočíselný, preškrtnúť ich a napísať na papier daný priemer. Dokážte, že pre každé $n\ge 3$ vieme postupovať tak, že na konci ostane na papieri len jedno nepreškrtnuté číslo.
(Aritmetický priemer dvoch čísel je ich súčet predelený dvomi.)

Ukážte, že medzi každou skupinou $8$ prirodzených čísel, ktorej súčet je $20$, je vždy nejaká skupina čísel, ktorej súčet je $4$.

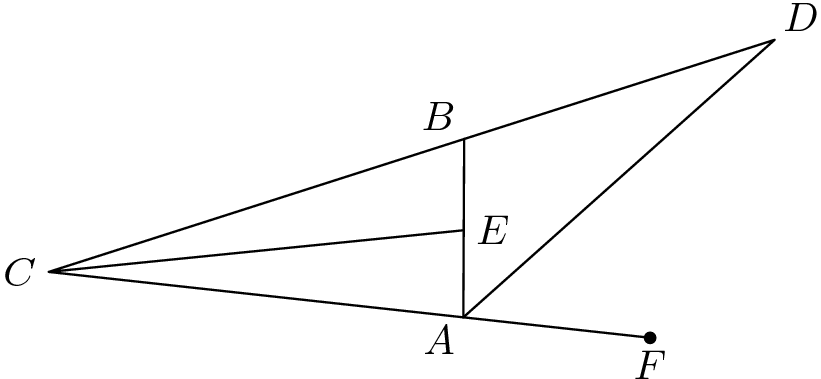
Problém znel: Na obrázku je trojuholník $ABC$, v ktorom $|\angle ABC| = 72^\circ$ a $|\angle CAB| = 84^\circ$. Bod $E$ leží na úsečke $AB$ tak, že úsečka $EC$ rozdeľuje uhol $BCA$ na dva zhodné. Bod $F$ leží na polpriamke $CA$ za bodom $A$. Bod $D$ leží na polpriamke $CB$ tak, že $DA$ rozdeľuje uhol $BAF$ na zhodné uhly. Dokážte, že $|AD| = |CE|$.

Kormidelník si obzeral svoj podiel z najnovšieho lupu. Jeho súčasťou boli aj štyri strieborné mince neznámej meny: jednokoruna, dvojkoruna, trojkoruna a päťkoruna. Kormidelník očakával, že budú vážiť po poradí $1$, $2$, $3$ a $5$ gramov. Od svojich druhov sa však dozvedel, že hmotnosť jednej z nich sa o niečo líši od predpokladanej hmotnosti, hoci ostatné zodpovedajú presne. Ako má kormidelník zistiť pomocou rovnoramenných váh bez závaží, ktorá minca nemá predpovedanú hmotnosť? Na miskách váh sa môžu objaviť iba zmienené mince a kormidelník má z každej hodnoty práve jeden spomínaný kus. Do riešenia napíšte postup, ako má kormidelník vážiť, aby to s istotou zistil.

Súčin piatich prvočísel je šesťciferné číslo v tvare $\overline{ABCABC}$, kde $A$, $B$ a $C$ sú cifry (napríklad číslo $123123$ je v takomto tvare). Zistite hodnotu $A$, $B$ a $C$, ak viete, že jedno z týchto piatich prvočísel je $491$. Nájdite všetky možnosti a odôvodnite, že iné neexistujú.

Kapitán a dôstojník hrajú hru na plániku $5 \times 5$ (kapitán začína). V ťahoch sa striedajú, pričom kapitán vo svojom ťahu vyfarbí jednotkový štvorček (svojou farbou) a dôstojník vyfarbí $3 \times 1$ obdĺžnik (svojou farbou). Už zafarbené políčka sa nedajú farbiť znovu. Hra končí, keď dôstojník už nevie urobiť ťah – zvyšné nevyfarbené políčka vtedy zafarbí kapitán. Vyhráva ten z nich, ktorý má na konci hry viac políčok vyfarbených svojou farbou. Rozhodnite, či existuje pre niektorého z nich výherná stratégia.
(Výhernou stratégiou rozumieme návod, ako má hráč hrať, aby vždy vyhral, nech ten druhý hrá akokoľvek.)

Šibenica mala pôdorys v tvare lichobežníka $ABCD$ so základňami $AB$ a $CD$ (ktoré sú rovnobežné), pričom uhlopriečky $AC$ a $BD$ sú na seba kolmé. Ďalej uhly $BAC$ a $BDC$ boli zhodné. Aritmetický priemer dĺžok základní lichobežníka bol rovný $8$. Aký bol obsah celého lichobežníka $ABCD$?
(Aritmetický priemer dĺžok dvoch strán je ich súčet predelený dvomi.)