
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Matik, 38. ročník - Letný semester
Vzorové riešenia 1. série nájdeš v časopise Matik-38-5
Vzorové riešenia 2. série nájdeš v časopise Matik-38-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 17. marec 2025 20:00:00
1. Rod Kamenných pozostáva zo šiestich súrodencov: Šuter, Balvan, Megaskala, Okruhliak, Ploskáč a Kváder. Vieme, že práve dvaja z nich majú kľúč od truhlice plnej korunovačných klenotov. Každého z nich sme sa spýtali, ktorí z nich to sú, a dostali sme nasledovné odpovede:
- Šuter vraví, že je to Megaskala a Balvan.
- Balvan vraví, že je to Šuter a Megaskala.
- Megaskala vraví, že je to Balvan a Okruhliak.
- Okruhliak vraví, že je to Ploskáč a Megaskala.
- Ploskáč vraví, že je to Kváder a Okruhliak.
- Kváder nepovedal nič.
2. Nožnicovci sú zo všetkých rodov najmúdrejší a nedávno na svojom hrade inštalovali výťah, aby sa mohli jednoduchšie prepravovať medzi svojimi poschodiami. Poschodia boli očíslované postupne číslami \(1\), \(2\), \(3\),... a výťah sa ovláda len pomocou dvoch tlačidiel - to ľavé vás posunie o dve poschodia nadol, to pravé vás posunie na poschodie s dvojnásobným číslom. Ostrostrihač sa chce výťahom previezť tak, aby zastal na každom poschodí. Existuje poschodie, na ktorom môže začať tak, aby sa mu to podarilo, ak
- počet poschodí je \(10\),
- počet poschodí je \(20\)?
3. Papierovci obývajú zámok v tvare rovnobežníka \(ABCD\), pre ktorý platí, že \(|AB|=2 \cdot |BC|\). Hlavný vchod \(V\) sa nachádza v strede strany \(CD\). Určte veľkosť uhla \(AVB\).
4. Kachličková podlaha v sídle rodu Kamenných tvorí prázdnu tabuľku \(3 \times 51\). Balvan chce do nej nakresliť kriedou čísla, pričom sa riadi nasledujúcimi pravidlami:
- V tabuľke sa musí nachádzať každé z čísel \(1\), \(2\), \(3\),..., \(153\).
- V ľavom dolnom políčku tabuľky má byť číslo \(1\).
- Políčka po sebe idúcich čísel susedia stranou.
5. Členovia rodu Papierových sa vyznačujú tým, že každý má na sebe napísané nejaké kladné celé číslo. Príslušníci s po sebe idúcimi číslami od \(1\) do \(n\) sa zoradili do radu tak, aby pre každú trojicu ľudí stojacich pri sebe platilo, že súčet ich čísel je deliteľný číslom toho najľavejšieho z nich troch. Koľko najviac Papierovcov môže takto stáť za sebou, aby ešte navyše platilo, že posledný člen v rade má nepárne číslo?
6. Bratia Okruhliak a Kváder vyrobili špeciálny drevený stôl v tvare konvexného štvoruholníka. Tento štvoruholník si označíme \(ABCD\). Uhly \(DAB\) a \(ABC\) sú ostré a ich osi sa pretínajú v bode \(E\). Dokážte, že ak \(|AD| + |BC| = |AB|\), tak
\[
|\sphericalangle DEC| = |\sphericalangle DAB| + |\sphericalangle ABC|.
\]
Úlohu neriešte meraním.
Vzorové riešenia 1. série nájdeš v časopise Matik-38-5
Vzorové riešenia 2. série nájdeš v časopise Matik-38-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 14. apríl 2025 20:00:00
1. Deviati súrodenci z rodu Papierovcov majú na sebe navzájom rôzne čísla od \(1\) do \(9\). Ich jedáleň má podlahu z dlaždíc o rozmere \(3 \times 3\). Vedia sa postaviť každý na jednu dlaždicu tak, aby súčet čísel každej stranou susediacej dvojice súrodencov bolo prvočíslo? Ak áno, uveďte príklad takého rozostavenia. Ak nie, zdôvodnite prečo.
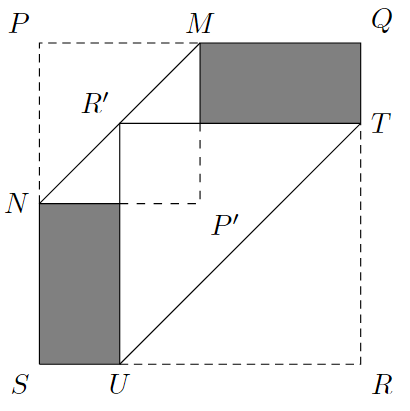
2. Knihovec objavil origami a chce si skúsiť niečo poskladať. Má pred sebou štvorcový papier označený \(PQRS\), ktorý má stranu dĺžky \(40\) cm. Bod \(M\) je stred strany \(PQ\) a bod \(N\) je stred strany \(PS\). Papier preložíme pozdĺž úsečky \(MN\). Bod \(P\) sa dotkne papiera v bode \(P'\). Bod \(T\) leží na strane \(QR\) a bod \(U\) leží na strane \(SR\) tak, že \(TU\) je rovnobežná s \(MN\). Ak papier preložíme pozdĺž \(TU\), bod \(R\) sa dotkne papiera v bode \(R'\), pričom \(R'\) leží na \(MN\). Lenže Knihovec má radšej počítanie ako skladanie origami a viac ho zaujíma, aký je obsah šesťuholníka \(NMQTUS\), ktorý vznikol. Pomôžte mu ho vyrátať!

3. Na plochozemi žije rod Papierových, ktorí vždy hovoria pravdu, a rod Nožnicovcov, ktorí vždy klamú. Na hranie stolného tenisu boli všetci príslušníci týchto dvoch rodov rozdelení do dvoch tímov \(A\) a \(B\), pričom \(A\) malo viac členov ako \(B\). Hru začali dvaja hráči z rôznych tímov. Po každej hre prehrávajúci hráč hru navždy opustil a nahradil ho iný (ešte nehrajúci) člen jeho tímu. Družstvo prehralo, ak všetci jeho členovia opustili hru. Po turnaji sa každého člena tímu \(A\) opýtali: "Je pravda, že si v akejkoľvek hre prehral s príslušníkom rodu Nožnicovcov?" a každého člena tímu B sa spýtali: "Je pravda, že si porazil aspoň dvoch Papierových?" Všetky odpovede sa ukázali ako kladné. Ktorý tím vyhral - \(A\) alebo \(B\)? Zdôvodni.
4. Kamaráti Šuter a Balvan našli zaujímavý kameň v tvare trojuholníka a chcú ho preskúmať. Trojuholník si označili \(ABC\), kde dĺžka strany \(AB\) je \(4\) a dĺžka strany \(BC\) je \(2\). Bod \(D\) nech leží na \(AB\) vo vzdialenosti \(3\) od bodu \(A\). Dokážte, že kolmica na \(AB\) prechádzajúca bodom \(D\), os uhla \(ABC\) a os strany \(BC\) sa pretínajú v jednom bode. Úlohu neriešte rysovaním.
5. Knihovec a Ostrihovač hrajú hru na tabuľke \(7 \times 7\) a striedajú sa v ťahoch. Knihovec má červený kamienok v dolnom ľavom a hornom pravom rohu, Ostrihovač zasa čierny kamienok v dolnom pravom a hornom ľavom rohu. V svojom ťahu si môže hráč vybrať jeden zo svojich dvoch kamienkov a pohne s ním na susedné voľné políčko, ktoré s tým pôvodným susedilo stranou. Začína Knihovec a vyhráva vtedy, keď sa mu po konečnom počte ťahov podarí dostať svoje kamienky na dve políčka, ktoré susedia stranou. Má Knihovec výhernú stratégiu alebo mu v tom vie Ostrihovač zabrániť? Výherná stratégia je postup, podľa ktorého keď jeden hráč hrá, tak vyhrá bez ohľadu na ťahy súpera.
6. Do školy chodí \(1085\) detí zo všetkých rodov. Každé dieťa pozná minimálne \(33\) ďalších detí tejto školy tak, že poznania sú vzájomné. Dokážte, že vieme okolo stola posadiť \(4\) deti z tejto školy tak, že každé pozná oboch svojich susedov.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...